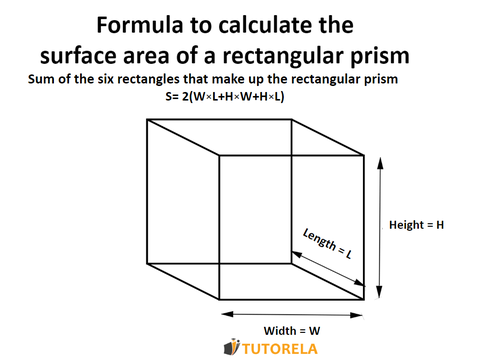
Rectangular Prisms are made up of different rectangles. When faced with an exercise or exam that asks you to calculate the surface area of a rectangular Prism, use the formula below.
Surface Area of a Cuboid - Examples, Exercises and Solutions
The formula: how to calculate the area of a rectangular prism (rectangular orthohedron)?
S= surface area
Suggested Topics to Practice in Advance
Practice Surface Area of a Cuboid
A cuboid has the dimensions shown in the diagram below.
Which rectangles form the cuboid?
A cuboid is shown below:
What is the surface area of the cuboid?
Look at the cuboid below.
What is the surface area of the cuboid?
Look at the cuboid below.
What is its surface area?
Look at the the cuboid below.
What is its surface area?
Examples with solutions for Surface Area of a Cuboid
Exercise #1
A cuboid has the dimensions shown in the diagram below.
Which rectangles form the cuboid?
Video Solution
Step-by-Step Solution
Every cuboid is made up of rectangles. These rectangles are the faces of the cuboid.
As we know that in a rectangle the parallel faces are equal to each other, we can conclude that for each face found there will be two rectangles.
Let's first look at the face painted orange,
It has width and height, 5 and 3, so we already know that they are two rectangles of size 5x6
Now let's look at the side faces, they also have a height of 3, but their width is 6,
And then we understand that there are two more rectangles of 3x6
Now let's look at the top and bottom faces, we see that their dimensions are 5 and 6,
Therefore, there are two more rectangles that are size 5x6
That is, there are
2 rectangles 5X6
2 rectangles 3X5
2 rectangles 6X3
Answer
Two 5X6 rectangles
Two 3X5 rectangles
Two 6X3 rectangles
Exercise #2
A cuboid is shown below:
What is the surface area of the cuboid?
Video Solution
Step-by-Step Solution
Remember that the formula for the surface area of a cuboid is:
(length X width + length X height + width X height) 2
We input the known data into the formula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Answer
62
Exercise #3
Look at the cuboid below.
What is the surface area of the cuboid?
Video Solution
Step-by-Step Solution
Let's see what rectangles we have:
8*5
8*12
5*12
Let's review the formula for the surface area of a rectangular prism:
(length X width + length X height + width X height) * 2
Now let's substitute all this into the exercise:
(8*5+12*8+12*5)*2=
(40+96+60)*2=
196*2= 392
This is the solution!
Answer
392 cm²
Exercise #4
Look at the cuboid below.
What is its surface area?
Video Solution
Step-by-Step Solution
We identified that the faces are
3*3, 3*11, 11*3
As the opposite faces of an cuboid are equal, we know that for each face we find there is another face, therefore:
3*3, 3*11, 11*3
or
(3*3, 3*11, 11*3 ) *2
To find the surface area, we will have to add up all these areas, therefore:
(3*3+3*11+11*3 )*2
And this is actually the formula for the surface area!
We calculate:
(9+33+33)*2
(75)*2
150
Answer
150
Exercise #5
Look at the the cuboid below.
What is its surface area?
Video Solution
Step-by-Step Solution
First, we recall the formula for the surface area of a cuboid:
(width*length + height*width + height*length) *2
As in the cuboid the opposite faces are equal to each other, the given data is sufficient to arrive at a solution.
We replace the data in the formula:
(8*5+3*5+8*3) *2 =
(40+15+24) *2 =
79*2 =
158
Answer
158
Identify the correct 2D pattern of the given cuboid:
Look at the cuboid of the figure.
Its surface area is 122 cm².
What is the width of the cuboid?
An unfolded cuboid is shown below.
What is the surface area of the cuboid?
Given that the volume of the cuboid is equal to 72 cm³
The length of the cuboid is equal to 6 cm and the height is equal to half the length.
Calculate the surface of the cuboid
Which dimensions may represent a cuboid?
Exercise #6
Identify the correct 2D pattern of the given cuboid:
Step-by-Step Solution
Let's go through the options:
A - In this option, we can observe that there are two flaps on the same side.
If we try to turn this net into a box, we should obtain a box where on one side there are two faces one on top of the other while the other side is "open",
meaning this net cannot be turned into a complete and full box.
B - This net looks valid at first glance, but we need to verify that it matches the box we want to draw.
In the original box, we see that we have four flaps of size 9*4, and only two flaps of size 4*4,
if we look at the net we can see that the situation is reversed, there are four flaps of size 4*4 and two flaps of size 9*4,
therefore we can conclude that this net is not suitable.
C - This net at first glance looks valid, it has flaps on both sides so it will close into a box.
Additionally, it matches our drawing - it has four flaps of size 9*4 and two flaps of size 4*4.
Therefore, we can conclude that this net is indeed the correct net.
D - In this net we can see that there are two flaps on the same side, therefore this net will not succeed in becoming a box if we try to create it.
Answer
Exercise #7
Look at the cuboid of the figure.
Its surface area is 122 cm².
What is the width of the cuboid?
Video Solution
Step-by-Step Solution
To solve the problem, let's recall the formula for calculating the surface area of a cube:
(width*length + height*width + height*length) *2
Let's substitute the known values into the formula, labelling the missing side X:
2*(3*7+7*X+3*X) = 122
2*(21+7x+3x) = 122
2(21+10x) = 122
Let's now expand the parentheses:
42+20x=122
Now we move terms:
20x=122-42
20x=80
Finally, simplify:
x=4
And that's the solution!
Answer
4 cm
Exercise #8
An unfolded cuboid is shown below.
What is the surface area of the cuboid?
Video Solution
Step-by-Step Solution
To calculate the surface area of the rectangular prism, we will need to identify its three faces (each face appears twice):
1*3
1*8
3*8
The formula for the surface area of a rectangular prism is the sum of all the areas of the faces, that is:
We replace the data in the formula:
2*(1*3+1*8+3*8)=
2*(3+8+24) =
2*35 =
70
And this is the solution!
Answer
70
Exercise #9
Given that the volume of the cuboid is equal to 72 cm³
The length of the cuboid is equal to 6 cm and the height is equal to half the length.
Calculate the surface of the cuboid
Video Solution
Step-by-Step Solution
The first step is to calculate the relevant data for all the components of the box.
The length of the box = 6
Given that the height of a cuboid is equal to half its length we are able to deduce the height of the box as follows : 6/2= 3
Hence the height = 3
In order to determine the width, we insert the known data into the formula for the volume of the box:
height*length*width = volume of the cuboid.
3*6*width = 72
18*width=72
We divide by 18:
Hence the width = 4
We are now able to return to the initial question regarding the surface of the cuboid.
Remember that the formula for the surface area is:
(height*length+height*width+length*width)*2
We insert the known data leaving us with the following result:
(3*6+4*3+4*6)*2=
(12+24+18)*2=
(54)*2=
108
Answer
108 cm²
Exercise #10
Which dimensions may represent a cuboid?
Step-by-Step Solution
There is no limitation or rule regarding the dimensions that a cuboid can have.
Therefore the correct answer is D.
Answer
All of the above.
Calculate the surface area of the orthohedron below using the data in the diagram.
What is the surface area of the cuboid in the figure?
A cuboid has a surface area of 102.
Calculate X.
A rectangular prism has a square base measuring 25 cm.
It has a height is equal to 3 cm.
Calculate the surface area of the rectangular prism.
Calculate the surface area of the box shown in the diagram.
Pay attention to the units of measure!
Exercise #11
Calculate the surface area of the orthohedron below using the data in the diagram.
Video Solution
Answer
62
Exercise #12
What is the surface area of the cuboid in the figure?
Video Solution
Answer
4940
Exercise #13
A cuboid has a surface area of 102.
Calculate X.
Video Solution
Answer
3
Exercise #14
A rectangular prism has a square base measuring 25 cm.
It has a height is equal to 3 cm.
Calculate the surface area of the rectangular prism.
Video Solution
Answer
110
Exercise #15
Calculate the surface area of the box shown in the diagram.
Pay attention to the units of measure!
Video Solution
Answer
724