Identify the correct 2D pattern of the given cuboid: 4 4 4 4 4 4 9 9 9

9 9 9 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4

4 4 4 4 4 4 9 9 9 4 4 4 4 4 4 4 4 4 4 4 4

4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 9 9 9 4 4 4 9 9 9

9 9 9 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4

4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 9 9 9

Three-Dimensional Figures

Three-dimensional figures

What are three-dimensional figures?

So far we have worked with common two-dimensional figures such as the square or the triangle.
Three-dimensional figures are those that extend into the third dimension, meaning that in addition to length and width, they also have height (that is, the figure has depth).

What differences do three-dimensional figures have?

Three-dimensional figures have several definitions that we will see next:
Below is a three-dimensional figure that we will use to learn each definition - The cube:

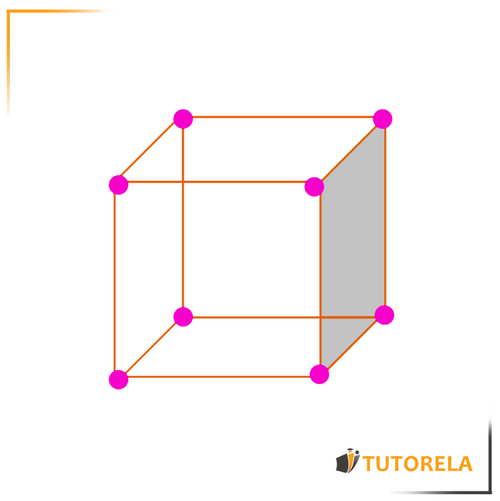
Face: it is the flat side of a three-dimensional figure
In the cube we have here, there are 6 faces (one of them is painted gray)
Edge: these are the lines that connect one face to another in a three-dimensional figure
In the cube we have here, there are 12 edges (painted green)
Vertex: it is the point that connects the edges
In the cube we have here, there are 8 vertices (painted orange)

Volume: it is the amount of space contained within a three-dimensional figure.
The units of measurement are $cm^3$ .

Detailed explanation

Start practice

Test yourself on cuboids!

Look at the cuboid below:

What is the volume of the cuboid?

Practice more now

Cuboid

The cuboid is a three-dimensional figure composed of 6 rectangles.

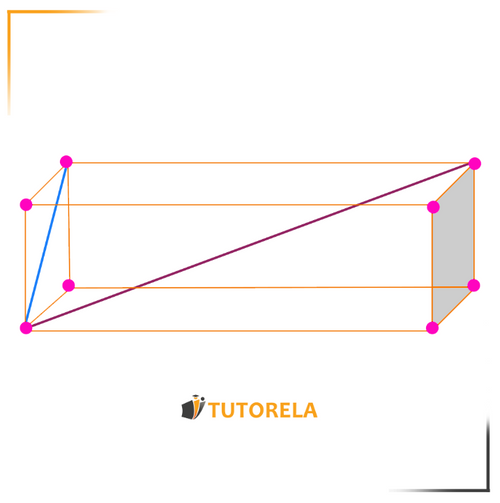
Each cuboid has:

6 faces: the rectangles that make up the cuboid - three pairs of rectangles that can be different from each other.
12 edges: the edges of the cuboid (divided into length, width, and height) - marked in green
8 vertices: the points where the edges meet - marked in orange

You can learn more about the parts of the cuboid by reading this article

Face diagonals:

The diagonals that go from one vertex to another on the same face as long as the vertices belong to the same face - marked in blue

Diagonal of the cuboid:

The diagonals that go from one vertex to another on different faces, as long as the 2 vertices belong to the same face - marked in red

Volume of the cuboid

The volume of the rectangular prism is ( \times \~the~width~\times \~the~length\~the~height\)

For more information about the volume of the rectangular prism click here

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Look at the cuboid below.

What is the surface area of the cuboid?

Question 2

A cuboid is shown below:

What is the surface area of the cuboid?

Question 3

Given the cuboid of the figure:

What is its volume?

Surface area of a cuboid

The formula to find the surface area is(width\times length + height\times width+ height\times length)\times \2

You can read again about the surface area of a rectangular prism by clicking here

Lateral area of a cuboid

It is the sum of the area of the four lateral rectangles (without the bases).
The lateral area of a cuboid can be calculated with the following formula:
a- Length
b- Width
h- Height

2\times \ah+2\times \bh= lateral~area~of~a~cuboid

You can read again about the lateral area of a cuboid by clicking here
For more information about the cuboid click here

Do you know what the answer is?

Question 1

Calculate the volume of the cuboid

If its length is equal to 7 cm:

Its width is equal to 3 cm:

Its height is equal to 5 cm:

Question 2

Shown below is a cuboid with a length of 8 cm.

Its width is 2 cm and its height is 4 cm.

Calculate the volume of the cube.

Question 3

A cuboid is 9 cm long, 4 cm wide, and 5 cm high.

Calculate the volume of the cube.

Cylinder

The cylinder is a three-dimensional figure composed of two identical parallel circles called bases, between which the lateral area expands.

Other properties:

The distance between the two bases is constant and is called the height of the cylinder - we will mark it with an $H$
The radius of both bases is equal, we will mark it with an $R$

Volume of the cylinder

The volume contained within the cylinder is usually denoted by $V$ .
Formula to calculate the volume of the cylinder:
$π\times \R^2\times \H = V$

When:

$π$ = PI ( $3.14$ )
$R$ = Radius of the base
$H$ = Height of the cylinder

For more information about the volume of the cylinder click here

Check your understanding

Question 1

Below is a cuboid with a length of

8 cm.

Its width is 2 cm and its height is

4 cm.

Calculate the volume of the cube.

Question 2

A cuboid has a length of is 9 cm.

It is 4 cm wide and 5 cm high.

Calculate the volume of the cube.

Question 3

Look at the the cuboid below.

What is its surface area?

Total surface area of a cylinder

The total area of the lateral surface and the two bases - we will denote it with $A$
We will use the formula:

$2πR\times \H+2π\times \R^2$

When:

$π$ = PI ( $3.14$ )
$R$ = Radius of the base
$H$ = Height of the cylinder

For more information click here

Lateral area of a cylinder

Only the lateral area without the bases. We will denote it with $S$
We will use the formula:

2πR\times \H

When:

$π$ = PI ( $3.14$ )
$R$ = Radius of the base
$H$ = Height of the cylinder

For more information about the cylinder click here

Do you think you will be able to solve it?

Question 1

Look at the cuboid below.

What is its surface area?

Question 2

An unfolded cuboid is shown below.

What is the surface area of the cuboid?

Question 3

A cuboid has the dimensions shown in the diagram below.

Which rectangles form the cuboid?

Prism

The right triangular prism is a three-dimensional figure that is composed of 2 triangles and 3 rectangles:

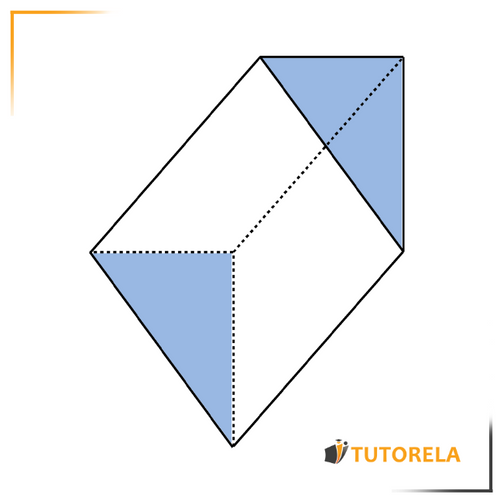
Base of the prism: the 2 triangles that compose it will always be identical (marked in orange).
The triangles can be isosceles, scalene, or equilateral.
To delve deeper into the topic of the bases of the prism click here
Faces of the prism: the 3 rectangles that make up the lateral faces - they will not necessarily be identical.
Heights of the prism: the three lines that join the bases - always have the same length.
For more information about the heights of the prism click here

Let's practice!
In a right triangular prism, are the triangular bases always identical?
Solution:
Yes! The triangles, which are actually the bases, are always the same.
Exercise:
How many heights are there in a right triangular prism?
Are they identical?
Solution:
There are 3 heights in a right triangular prism and they always have the same length.
Exercise:
Do the three rectangles that make up the lateral faces of the prism have to be identical?
Solution:
No.
The edges of the triangle do not necessarily have to be equal and this could create different rectangles.

Volume of the right triangular prism

The volume of the prism is usually expressed through the following formula:
$V= S \cdot H$

$S$ = Area of the base
$H$ = Height of the prism

You can read again about the area of the prism by clicking here

Test your knowledge

Question 1

Identify the correct 2D pattern of the given cuboid:

Question 2

An orthohedron has the dimensions: 4, 7, 10.

How many rectangles is it formed of and what are their dimensions?

Question 3

Look at the cuboid below:

What is the volume of the cuboid?

Area of a right triangular prism

The area of a right triangular prism is, in fact, the total sum of the surfaces of its two bases (the triangles) and its three lateral faces (the rectangles).

For more information about the area of the prism click here

Examples and exercises with solutions of three-dimensional figures

Exercise #1

Look at the cuboid below:

What is the volume of the cuboid?

Video Solution

Step-by-Step Solution

To determine the volume of a cuboid, we apply the formula:

Step 1: Identify the dimensions of the cuboid:
- Length ( $l$ ) = 12 cm
- Width ( $w$ ) = 8 cm
- Height ( $h$ ) = 5 cm
Step 2: Apply the volume formula for a cuboid:

The formula to find the volume ( $V$ ) of a cuboid is:

$V = l \times w \times h$

Step 3: Substitute the given dimensions into the formula and calculate: $V = 12 \times 8 \times 5$

Step 4: Perform the multiplication in stages for clarity:

First, calculate $12 \times 8 = 96$

Then multiply the result by 5: $96 \times 5 = 480$

Therefore, the volume of the cuboid is $\mathbf{480 \, \text{cm}^3}$ .

Answer

480 cm³

Exercise #2

Look at the cuboid below.

What is the surface area of the cuboid?

Video Solution

Step-by-Step Solution

Let's see what rectangles we have:

8*5

8*12

5*12

Let's review the formula for the surface area of a rectangular prism:

(length X width + length X height + width X height) * 2

Now let's substitute all this into the exercise:

(8*5+12*8+12*5)*2=
(40+96+60)*2=
196*2= 392

This is the solution!

Answer

392 cm²

Exercise #3

A cuboid is shown below:

What is the surface area of the cuboid?

Video Solution

Step-by-Step Solution

Remember that the formula for the surface area of a cuboid is:

(length X width + length X height + width X height) 2

We input the known data into the formula:

2*(3*2+2*5+3*5)

2*(6+10+15)

2*31 = 62

Answer

Exercise #4

Given the cuboid of the figure:

What is its volume?

Video Solution

Step-by-Step Solution

To solve this problem, we'll calculate the volume of the cuboid using the given dimensions:

Step 1: Identify the dimensions
Step 2: Apply the volume formula for a cuboid
Step 3: Calculate the volume

Let's work through these steps:

Step 1: From the diagram, we are informed of two dimensions directly: the width $w = 5$ and the height $h = 4$ . The diagram also indicates the horizontal length (along the base) is $l = 9$ .

Step 2: To find the volume of the cuboid, we use the formula:
$\text{Volume} = \text{length} \times \text{width} \times \text{height}.$

Step 3: Substituting the identified dimensions into the formula, we have:
$\text{Volume} = 9 \times 5 \times 4.$

Calculating this, we find:
$9 \times 5 = 45,$
$45 \times 4 = 180.$

Therefore, the volume of the cuboid is $180$ cubic units.

This corresponds to choice \#4: 180.

Answer

180

Exercise #5

Calculate the volume of the cuboid

If its length is equal to 7 cm:

Its width is equal to 3 cm:

Its height is equal to 5 cm:

Video Solution

Step-by-Step Solution

The formula to calculate the volume of a cuboid is:

height*length*width

We replace the data in the formula:

3*5*7

7*5 = 35

35*3 = 105

Answer

105 cm³

Do you know what the answer is?

Question 1

Look at the cuboid below.

What is the surface area of the cuboid?

Question 2

A cuboid is shown below:

What is the surface area of the cuboid?

Question 3

Given the cuboid of the figure:

What is its volume?

Start practice

Three-Dimensional Figures

Three-dimensional figures

What are three-dimensional figures?

What differences do three-dimensional figures have?

Test yourself on cuboids!

Cuboid

Each cuboid has:

Face diagonals:

Diagonal of the cuboid:

Volume of the cuboid

Surface area of a cuboid

Lateral area of a cuboid

Cylinder

Volume of the cylinder

Total surface area of a cylinder

Lateral area of a cylinder

Prism

Volume of the right triangular prism

Area of a right triangular prism

Examples and exercises with solutions of three-dimensional figures

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Cuboids