Extended Distributive Property - Examples, Exercises and Solutions

Let's simplify the given expression by opening the parentheses using the extended distribution law:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$

Note that in the formula template for the above distribution law, we take by default that the operation between the terms inside the parentheses is addition. Therefore we won't forget of course that the sign preceding the term is an inseparable part of it. We will also apply the rules of sign multiplication and thus we can present any expression in parentheses. We'll open the parentheses using the above formula, first as an expression where an addition operation exists between all terms. In this expression it's clear that all terms have a plus sign prefix. Therefore we'll proceed directly to opening the parentheses,

$$Let's begin:

$(\textcolor{red}{x}+\textcolor{blue}{4})(x+3)\\ \textcolor{red}{x}\cdot x+\textcolor{red}{x}\cdot3+\textcolor{blue}{4}\cdot x +\textcolor{blue}{4}\cdot3\\ x^2+3x+4x+12$

In calculating the above multiplications, we used the multiplication table and the laws of exponents for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$

In the next step we'll combine like terms, which we define as terms where the variable (or variables each separately), in this case x, have identical exponents .(In the absence of one of the variables from the expression, we'll consider its exponent as zero power given that raising any number to the power of zero yields 1) We'll apply the commutative property of addition, furthermore we'll arrange (if needed) the expression from highest to lowest power from left to right (we'll treat the free number as having zero power):
$\textcolor{purple}{x^2}\textcolor{green}{+3x}\textcolor{green}{+4x}+12\\ \textcolor{purple}{x^2}\textcolor{green}{+7x}+12$In the combining of like terms performed above, we highlighted the different terms using colors, and as emphasized before, we made sure that the sign preceding the term is an inseparable part of it,

Thus the correct answer is C.

Let's simplify the expression by opening the parentheses using the distributive property:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$

Therefore, the correct answer is (a).

To solve this problem, we'll apply the FOIL method for multiplying binomials:

• First: Multiply the first terms in each binomial: $(2x)(x) = 2x^2$.
• Outer: Multiply the outer terms in the product: $(2x)(3) = 6x$.
• Inner: Multiply the inner terms: $(y)(x) = xy$.
• Last: Multiply the last terms: $(y)(3) = 3y$.

Next, we combine these results to form the expanded expression:

$2x^2 + 6x + xy + 3y$.

Since terms $6x$ and $xy$ are not like terms, they cannot be combined, resulting in the final expression:

$2x^2 + xy + 6x + 3y$.

Upon reviewing the multiple-choice options, the correct answer is the expanded expression, choice 4: $2x^2 + xy + 6x + 3y$.

When we encounter a multiplication exercise of this type, we know that we must use the distributive property.

Step 1: Multiply the first factor of the first parentheses by each of the factors of the second parentheses.

Step 2: Multiply the second factor of the first parentheses by each of the factors of the second parentheses.

Step 3: Group like terms.

a * (c+3) =

a*c + a*3

4  * (c+3) =

4*c + 4*3

ac+3a+4c+12

There are no like terms to simplify here, so this is the solution!

To solve this problem, we'll perform a step-by-step expansion of the expression $(x+13)(y+4)$ using the distributive property:

• Step 1: Multiply the first terms $(x \cdot y) = xy$.
• Step 2: Multiply the outer terms $(x \cdot 4) = 4x$.
• Step 3: Multiply the inner terms $(13 \cdot y) = 13y$.
• Step 4: Multiply the last terms $(13 \cdot 4) = 52$.

After completing these steps, combine the results:

$xy + 4x + 13y + 52$

This is the final expanded form of the expression. By comparing with the given choices, the correct answer is:

$xy + 4x + 13y + 52$

Therefore, the correct choice is option 3.

Let's simplify the given expression, using the expanded distribution law in order to open the parentheses :

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$

Note that in the formula template for the above distribution law, we take by default that the operation between the terms inside of the parentheses is addition. We must remember that the sign preceding the term is an inseparable part of it. We'll also apply the rules of sign multiplication and thus we can present any expression inside of the parentheses. We'll open the parentheses using the above formula, first as an expression where addition operation exists between all terms:

$(x-8)(x+y)\\ (\textcolor{red}{x}+\textcolor{blue}{(-8)})(x+y)\\$Proceed to open the parentheses:

$(\textcolor{red}{x}+\textcolor{blue}{(-8)})(x+y)\\ \textcolor{red}{x}\cdot x+\textcolor{red}{x}\cdot y+\textcolor{blue}{(-8)}\cdot x +\textcolor{blue}{(-8)}\cdot y\\ x^2+xy-8x -8y$

In calculating the above multiplications, we used the multiplication table and the laws of exponents for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$

Note that in the expression that we obtained in the last stage there are four different terms, this is due to the fact that there isn't even one pair of terms where the variables (different ones) have the same exponent. Additionally the expression is already organized therefore the expression that we obtain is the final and most simplified form:
$\textcolor{purple}{ x^2}\textcolor{green}{+xy}-8x \textcolor{orange}{-8y}\\$We highlighted the different terms using colors, and as emphasized before, we made sure that the sign preceding the term is an inseparable part of it,

Therefore the correct answer is answer A.

Let's simplify the given expression,using the extended distribution law to open the parentheses :

$(\textcolor{red}{t}+\textcolor{blue}{k})(c+d)=\textcolor{red}{t}c+\textcolor{red}{t}d+\textcolor{blue}{k}c+\textcolor{blue}{k}d$

Note that in the formula template for the above distribution law, we take as a default that the operation between terms inside of the parentheses is addition. Remember that the sign preceding the term is an inseparable part of it. Apply the rules of sign multiplication and we can present any expression inside of the parentheses. We'll open the parentheses by using the above formula, as an expression where addition operation exists between all terms:

$(12-x)(x-3) \\ (\textcolor{red}{12}+\textcolor{blue}{(-x)})(x+(-3))\\$Let's begin then with opening the parentheses:

$(\textcolor{red}{12}+\textcolor{blue}{(-x)})(x+(-3))\\ \textcolor{red}{12}\cdot x+\textcolor{red}{12}\cdot(-3)+\textcolor{blue}{(-x)}\cdot x +\textcolor{blue}{(-x)}\cdot(-3)\\ 12x-36-x^2 +3x$

In calculating the above multiplications, we used the multiplication table and the laws of exponents for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$

In the next step, we'll combine like terms which we define as terms where the variable (or variables each separately), in this case x, have identical exponents. (In the absence of one of the variables from the expression, we'll consider its exponent as zero power, given that raising any number to the zero power yields 1) Apply the commutative property of addition and proceed to arrange the expression from highest to lowest power from left to right (we'll treat the free number as having zero power):
$\textcolor{purple}{12x}\textcolor{green}{-36}-x^2\textcolor{purple}{+3x}\\ -x^2\textcolor{purple}{+12x+3x}\textcolor{green}{-36}\\ -x^2\textcolor{purple}{+15x}\textcolor{green}{-36}\\$In the combining of like terms performed above, we highlighted the different terms using colors, and as emphasized before, we made sure that the sign preceding the term remained an inseparable part of it,

We therefore got that the correct answer is answer A (we used the commutative property of addition to verify this).

Let's simplify the given expression, using the extended distribution law to open the parentheses :

$(\textcolor{red}{t}+\textcolor{blue}{b})(c+d)=\textcolor{red}{t}c+\textcolor{red}{t}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$

Note that in the formula template for the above distribution law, we take by default that the operation between the terms inside of the parentheses is addition. Remember that the sign preceding the term is an inseparable part of it. Apply the rules of sign multiplication so that we can present any expression in parentheses. We'll open the parentheses using the above formula, as an expression where addition operation exists between all terms. In this expression it's clear, all terms have a plus sign prefix.

Therefore we'll proceed directly to opening the parentheses as shown below:

$$:

$(\textcolor{red}{a}+\textcolor{blue}{15})(5+a)\\ \textcolor{red}{a}\cdot 5+\textcolor{red}{a}\cdot a+\textcolor{blue}{15}\cdot 5 +\textcolor{blue}{15}\cdot a\\ 5a+a^2+75+15a$

In calculating the above multiplications, we used the multiplication table and the laws of exponents for multiplication between terms with identical bases:

$x^m\cdot x^n=x^{m+n}$

In the next step we'll combine like terms, which we define as terms where the variable (or variables each separately), in this case a, have identical exponents. (In the absence of one of the variables from the expression, we'll consider its exponent as zero power, this is due to the fact that any number raised to the power of zero equals 1) Apply the commutative law of addition and arrange the expression from highest to lowest power from left to right (we'll treat the free number as power of zero):
$\textcolor{purple}{5a}\textcolor{green}{+a^2}+75\textcolor{purple}{+15a}\\ \textcolor{green}{a^2}\textcolor{purple}{+5a+15a}+75\\ \textcolor{green}{a^2}\textcolor{purple}{+20a}+75\\$In the combining of like terms performed above, we highlighted the different terms using colors, and as emphasized before, we made sure that the sign preceding the term is an inseparable part of it,

We therefore got that the correct answer is answer B.

To solve this problem, we'll use the distributive property, also known as the FOIL method when dealing with two binomials.

Let's expand the expression $(7+b)(a+9)$:

• First, apply the distributive property by multiplying each term in the first binomial by each term in the second binomial. This means we will have four operations:
• Step 1: Multiply $7$ by $a$. This gives $7a$.
• Step 2: Multiply $7$ by $9$. This gives $63$.
• Step 3: Multiply $b$ by $a$. This gives $ab$.
• Step 4: Multiply $b$ by $9$. This gives $9b$.

After performing these operations, the expression expands to:

$7a + 63 + ab + 9b$

Rearrange the terms in standard form for the final answer, which is:

$ab + 7a + 9b + 63$

Therefore, the solution to the problem is $ab + 7a + 9b + 63$.

To solve the problem and apply the distributive property correctly, follow these steps:

• Identify the expression, which is $a(b+c)$.
• Apply the distributive property: multiply $a$ by each term inside the parentheses.

Applying this, we get:

• $a \times b = ab$
• $a \times c = ac$

Combine these two products:

The simplified expression is: $ab + ac$.

This matches with answer choice 2: Yes, the answer $ab+ac$.

To solve this problem, we must determine if we can apply the distributive property to simplify the expression $(a+b)(c \cdot g)$.

The distributive property states that for any three terms, the expression $x(y+z)$ results in $xy + xz$. Here, we have the sum $(a + b)$ and the product $(c \cdot g)$.

We can treat $(c \cdot g)$ as a single term because it involves multiplication, which makes it like a single number or variable in terms of manipulating the expression algebraically. Therefore, using the distributive property, we distribute $(c \cdot g)$ over the terms within the parentheses:

• Step 1: Distribute $c \cdot g$ to $a$, yielding $acg$.
• Step 2: Distribute $c \cdot g$ to $b$, yielding $bcg$.

Hence, the simplified expression is:

$acg + bcg$.

Therefore, the correct answer, according to the choices provided, is:

No, $acg + bcg$.

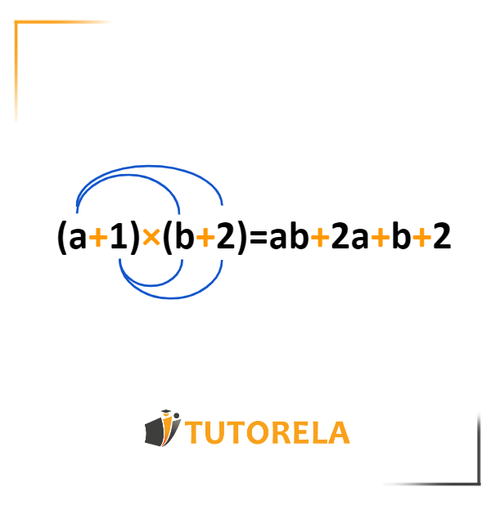
We simplify the given expression by opening the parentheses using the extended distributive property:

$(\textcolor{red}{x}+\textcolor{blue}{y})(t+d)=\textcolor{red}{x}t+\textcolor{red}{x}d+\textcolor{blue}{y}t+\textcolor{blue}{y}d$Keep in mind that in the distributive property formula mentioned above, we assume that the operation between the terms inside the parentheses is an addition operation, therefore, of course, we will not forget that the sign of the term's coefficient is ery important.

We will also apply the rules of multiplication of signs, so we can present any expression within parentheses that's opened with the distributive property as an expression with addition between all the terms.

In this expression we only have addition signs in parentheses, therefore we go directly to opening the parentheses,

$$We start by opening the parentheses:

$(\textcolor{red}{x}+\textcolor{blue}{c})(4+c)\\ \textcolor{red}{x}\cdot 4+\textcolor{red}{x}\cdot c+\textcolor{blue}{c}\cdot 4+\textcolor{blue}{c} \cdot c\\ 4x+xc+4c+c^2$To simplify this expression, we use the power law for multiplication between terms with identical bases:

$a^m\cdot a^n=a^{m+n}$

In the next step like terms come into play.

We define like terms as terms in which the variables (in this case, x and c) have identical powers (in the absence of one of the variables from the expression, we will refer to its power as zero power, this is because raising any number to the power of zero results in 1).

We will also use the substitution property, and we will order the expression from the highest to the lowest power from left to right (we will refer to the regular integer as the power of zero),

Keep in mind that in this new expression there are four different terms, this is because there is not even one pair of terms in which the variables (different) have the same power. Also it is already ordered by power, therefore the expression we have is the final and most simplified expression:$\textcolor{purple}{4x}\textcolor{green}{+xc}\textcolor{black}{+4c}\textcolor{orange}{+c^2 }\\ \textcolor{orange}{c^2 }\textcolor{green}{+xc}\textcolor{purple}{+4x}\textcolor{black}{+4c}\\$We highlight the different terms using colors and, as emphasized before, we make sure that the main sign of the term is correct.

We use the substitution property for multiplication to note that the correct answer is option A.

Let's remember the extended distributive property:

$(\textcolor{red}{a}+\textcolor{blue}{b})(c+d)=\textcolor{red}{a}c+\textcolor{red}{a}d+\textcolor{blue}{b}c+\textcolor{blue}{b}d$Note that the operation between the terms inside the parentheses is a multiplication operation:

$(a b)(c d)$Unlike in the extended distributive property previously mentioned, which is addition (or subtraction, which is actually the addition of the term with a minus sign),

Also, we notice that since there is a multiplication among all the terms, both inside the parentheses and between the parentheses, this is a simple multiplication and the parentheses are actually not necessary and can be remoed. We get:

$(a b)(c d)= \\ abcd$Therefore, opening the parentheses in the given expression using the extended distributive property is incorrect and produces an incorrect result.

Therefore, the correct answer is option d.

To solve this problem, we will expand the expression $(x-3)(x-6)$ using the distributive property, which involves the following steps:

• Step 1: Multiply the first terms of each binomial
  $(x)(x) = x^2$

• Step 2: Multiply the outer terms of the binomials
  $(x)(-6) = -6x$

• Step 3: Multiply the inner terms of the binomials
  $(-3)(x) = -3x$

• Step 4: Multiply the last terms of each binomial
  $(-3)(-6) = 18$

• Step 5: Combine all the products
  $x^2 - 6x - 3x + 18$

• Step 6: Combine like terms
  $-6x - 3x = -9x$, so we have
  $x^2 - 9x + 18$

Therefore, the expanded form of $(x-3)(x-6)$ is $\boxed{x^2 - 9x + 18}$.

Therefore, the solution to the problem is $x^2 - 9x + 18$. This corresponds to choice 1.

To solve the algebraic expression $(2y-3)(y-4)$, we will apply the distributive property, also known as the FOIL method for binomials. This involves multiplying each term in the first binomial by each term in the second binomial.

• Step 1: Multiply the first terms: $2y \times y = 2y^2$.
• Step 2: Multiply the outer terms: $2y \times -4 = -8y$.
• Step 3: Multiply the inner terms: $-3 \times y = -3y$.
• Step 4: Multiply the last terms: $-3 \times -4 = 12$.

Next, we combine all these results: $2y^2 - 8y - 3y + 12$.

Then, we combine the like terms $-8y$ and $-3y$ to get $-11y$.

Therefore, the expanded expression is $2y^2 - 11y + 12$.

This matches choice (3): $2y^2 - 11y + 12$.

Thus, the solution to the problem is $2y^2 - 11y + 12$.