Powers and Roots Practice Problems - Order of Operations

Master the order of operations with powers and roots through step-by-step practice problems. Learn PEMDAS/BODMAS rules with exponents and square roots.

📚Master Powers and Roots in Order of Operations
  • Apply PEMDAS/BODMAS rules correctly when solving expressions with exponents
  • Simplify powers and square roots before multiplication and division operations
  • Solve complex expressions with nested parentheses containing powers
  • Calculate expressions combining fractions, decimals, and exponential operations
  • Master the correct sequence: parentheses, powers/roots, multiplication/division, addition/subtraction
  • Build confidence with step-by-step solutions for combined operations problems

Understanding Order of Operations: (Exponents)

Complete explanation with examples

As part of combined operations, we learned that parentheses always come first.

Once solved, we can begin to simplify powers (or roots).

After simplifying them, we can continue solving the exercise according to the order of basic operations:

Firstly, the multiplications and divisions, and lastly, the additions and subtractions.

Let's refresh the order of operations:

  1. Parentheses
  2. Powers and roots
  3. Multiplications and divisions
  4. Additions and subtractions
Detailed explanation of the BODMAS/PEMDAS rule highlighting 'Order' (Exponents) with symbols like √x and x², crucial for solving complex arithmetic expressions step by step.

Detailed explanation

Practice Order of Operations: (Exponents)

Test your knowledge with 24 quizzes

\( 8-3^2:3= \)

Examples with solutions for Order of Operations: (Exponents)

Step-by-step solutions included
Exercise #1

20−33:3= 20-3^3:3=

Step-by-Step Solution

First, compute the power: 33=27 3^3 = 27 .

Next, divide: 27÷3=9 27 \div 3 = 9 .

Finally, subtract: 20−9=11 20 - 9 = 11 .

Answer:

11 11

Exercise #2

15−42:2= 15-4^2:2=

Step-by-Step Solution

First, compute the power: 42=16 4^2 = 16 .

Next, divide: 16÷2=8 16 \div 2 = 8 .

Finally, subtract: 15−8=7 15 - 8 = 7 .

Answer:

7 7

Exercise #3

10−52:5= 10-5^2:5=

Step-by-Step Solution

First, compute the power: 52=25 5^2 = 25 .

Next, divide: 25÷5=5 25 \div 5 = 5 .

Finally, subtract: 10−5=5 10 - 5 = 5 .

Answer:

5 5

Exercise #4

8−16×3= 8 - \sqrt{16} \times 3 =

Step-by-Step Solution

First, evaluate the square root: 16=4\sqrt{16}=4.

Then, follow the order of operations (PEMDAS/BODMAS):

1. Multiplication: 4×3=124 \times 3 = 12

2. Subtraction: 8−12=−48 - 12 = -4

So, the correct answer is −4 -4 .

Answer:

−4 -4

Exercise #5

7+49−5= 7 + \sqrt{49} - 5 =

Step-by-Step Solution

First, evaluate the square root: 49=7\sqrt{49}=7.

Then, follow the order of operations (PEMDAS/BODMAS):

1. Addition: 7+7=147 + 7 = 14

2. Subtraction: 14−5=914 - 5 = 9

So, the correct answer is 9 9 .

Answer:

9 9

Frequently Asked Questions

Everything you need to know about Order of Operations: (Exponents)

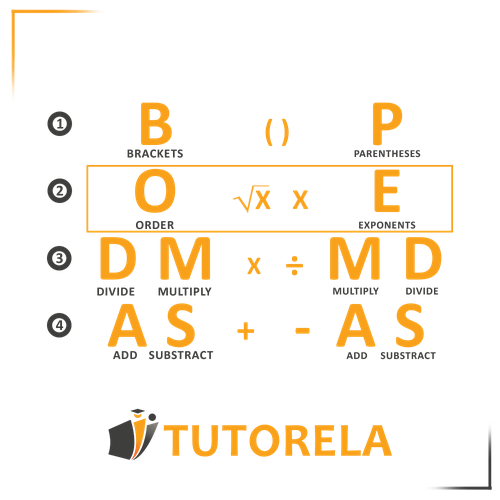
What is the correct order when solving expressions with powers and roots?

+
Follow PEMDAS/BODMAS: 1) Parentheses first, 2) Powers and roots second, 3) Multiplication and division from left to right, 4) Addition and subtraction from left to right. Powers and roots must always be calculated before any multiplication, division, addition, or subtraction operations.

How do you solve expressions with powers inside parentheses?

+
First solve everything inside the parentheses following the order of operations within them. If there's a power inside parentheses like (3²-1), calculate the power first (3²=9), then perform the subtraction (9-1=8). Only then can you use this result in the rest of the expression.

Why do powers come before multiplication in order of operations?

+
Powers represent repeated multiplication of a number by itself, so they're considered a higher-level operation than basic multiplication. This hierarchy ensures mathematical expressions are solved consistently and correctly, preventing different interpretations of the same problem.

What's the difference between solving 2+5×4² and (2+5)×4²?

+
In 2+5×4²: Calculate 4²=16 first, then 5×16=80, finally 2+80=82. In (2+5)×4²: Solve parentheses first (2+5=7), then the power 4²=16, finally multiply 7×16=112. Parentheses completely change the order and result.

How do you handle negative numbers with exponents in order of operations?

+
Be careful with notation: -3² equals -(3²) = -9, while (-3)² equals 9. The negative sign outside parentheses applies after calculating the power, but inside parentheses it's part of the base being raised to the power.

Can you solve powers and roots in the same step of order of operations?

+
Yes, powers and roots have equal precedence in the order of operations. When you have both in an expression, solve them from left to right in the order they appear, just like you would with multiplication and division.

What are common mistakes students make with powers in order of operations?

+
Common errors include: 1) Adding or multiplying before calculating powers, 2) Forgetting to apply order of operations inside parentheses, 3) Misinterpreting negative signs with exponents, 4) Not working from left to right when multiple operations have equal precedence.

How do fractional exponents work in order of operations?

+
Fractional exponents like (1/4)² follow the same order of operations rules. Calculate the power first: (1/4)² = 1/16, then continue with multiplication, division, addition, or subtraction as needed. The fraction inside parentheses is treated as a single base.

More Order of Operations: (Exponents) Questions

Click on any question to see the complete solution with step-by-step explanations

Powers and Roots

Calculate (2/3)³: Finding the Cube of a Fraction Solve: 6 + Square Root of 64 - 4 Expression Evaluation Solve 18² - (100 + √9): Mixed Operations Expression Solve 2×(√36 + 9): Order of Operations with Square Root Solve 2×(3³ + √144): Order of Operations Practice

Continue Your Math Journey

Master Order of Operations: (Exponents) first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

The Order of Basic Operations: Addition, Subtraction, and Multiplication

Topics Learned in Later Sections

Order of Operations: RootsOrder of Operations - Exponents and RootsOrder of Operations with ParenthesesDivision and Fraction Bars (Vinculum)The Numbers 0 and 1 in OperationsNeutral Element (Identity Element)Order or Hierarchy of Operations with FractionsMultiplicative InverseSpecial cases (0 and 1, reciprocals, fraction line)The Order of Operations

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Complete the missing numbers Exercises with fractions Identify the greater value Parentheses within parentheses Small Numbers Solving an exercise Solving the equation Solving the problem The perimeter of a square True / false Using fractions Using parentheses Using powers