Difference of Squares Formula
The difference of squares formula is another key algebraic shortcut that simplifies expressions involving two squared terms subtracted from each other. It is written as:
This formula skips the need for full expansion and directly factors the expression. It works for both numerical and algebraic expressions, making it versatile in solving equations and simplifying terms. That is, when we encounter two numbers with a minus sign between them, that is, the difference and they will be in parentheses and raised as a squared expression, we can use this formula.
For the full expansion would be:
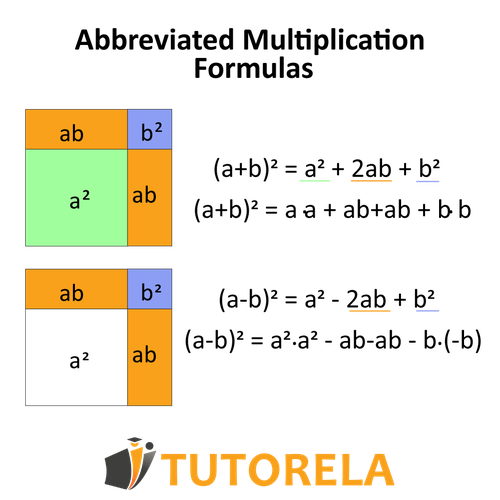
Example:









