A linear function, as it is called, is an algebraic expression that represents the graph of a straight line.
When we talk about functions, it's important to highlight that the graphs of functions are represented in an axis system where there is a horizontal axis and a vertical axis .
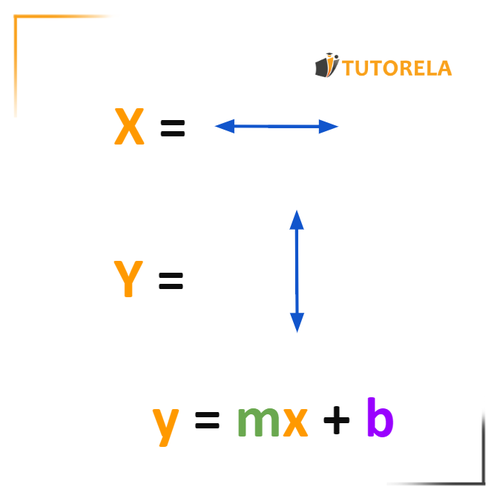
Linear functions can be expressed by the expressions or , where m represents the slope of the line while (when it exists) represents the y-intercept.
To plot a linear function, all we need are points. If the linear function is given, you can substitute a value for and obtain the corresponding value.
