Linear Function y=mx+b: Understanding the concept of slope

Determine the slope of a linear functionCalculate the slope from a tableConverting between graphs and equationsIncrease and decrease in relation to slopeCalculate the slope from two pointsDetermine whether the slope on the graph is positive or negativeUsing slope for geometric problems
Question 1

Which best describes the function below?

\( y=2-3x \)

Question 2

Calculate the slope of the line that passes through the points \( (4,1),(2,5) \).

Question 3

What is the slope of a straight line that passes through the points \( (0,0),(-8,2) \)?

Question 4

A linear function has a slope of -3 and passes through the point \( (-6,-3) \).

Choose the equation that represents the function.

Question 5

A linear function with a slope of 6 passes through the point \( (1,1) \).

Which equation represents the function?

Examples with solutions for Linear Function y=mx+b: Understanding the concept of slope

Exercise #1

Which best describes the function below?

y=2−3x y=2-3x

Video Solution

Step-by-Step Solution

Remember that the rate of change equals the slope.

In this function:

m=−3 m=-3

Therefore, the function is decreasing.

Answer

The function is decreasing.

Exercise #2

Calculate the slope of the line that passes through the points (4,1),(2,5) (4,1),(2,5) .

Video Solution

Step-by-Step Solution

Remember the formula for calculating a slope using points:

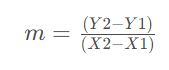
Now, replace the data in the formula with our own:

(5−1)(2−4)=4−2=−2 \frac{(5-1)}{(2-4)}=\frac{4}{-2}=-2

Answer

-2

Exercise #3

What is the slope of a straight line that passes through the points (0,0),(−8,2) (0,0),(-8,2) ?

Video Solution

Step-by-Step Solution

To solve the problem, remember the formula to find the slope using two points

 

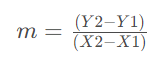
Now, we replace the given points in the calculation:

 (0−2)(0−(−8)=−28=−14 \frac{(0-2)}{(0-(-8)}=\frac{-2}{8}=-\frac{1}{4}

Answer

−14 -\frac{1}{4}

Exercise #4

A linear function has a slope of -3 and passes through the point (−6,−3) (-6,-3) .

Choose the equation that represents the function.

Video Solution

Answer

y=−3x−21 y=-3x-21

Exercise #5

A linear function with a slope of 6 passes through the point (1,1) (1,1) .

Which equation represents the function?

Video Solution

Answer

y=6x−5 y=6x-5

Question 1

A linear function has a slope of 1 and passes through the point \( (6,13) \).

Choose the equation that represents this function.

Question 2

A linear function with a slope of 6 passes through the point \( (1,-4) \).

Which equation represents the function?

Question 3

A linear function with a slope of 5 passes through the point \( (2,4) \).

Choose the equation that represents this function.

Question 4

What is the slope of a straight line that passed through the points \( (0,4),(-5,6) \)?

Question 5

Calculate the slope of a straight line that passes through the points \( (-6,1),(2,4) \).

Exercise #6

A linear function has a slope of 1 and passes through the point (6,13) (6,13) .

Choose the equation that represents this function.

Video Solution

Answer

y=x+7 y=x+7

Exercise #7

A linear function with a slope of 6 passes through the point (1,−4) (1,-4) .

Which equation represents the function?

Video Solution

Answer

y=6x−10 y=6x-10

Exercise #8

A linear function with a slope of 5 passes through the point (2,4) (2,4) .

Choose the equation that represents this function.

Video Solution

Answer

y=5x−6 y=5x-6

Exercise #9

What is the slope of a straight line that passed through the points (0,4),(−5,6) (0,4),(-5,6) ?

Video Solution

Answer

−25 -\frac{2}{5}

Exercise #10

Calculate the slope of a straight line that passes through the points (−6,1),(2,4) (-6,1),(2,4) .

Video Solution

Answer

38 \frac{3}{8}