Parabola Increasing Decreasing Intervals Practice Problems

Master finding increasing and decreasing intervals of parabolas with step-by-step practice problems. Learn to identify vertex points and analyze function behavior.

📚Practice Finding Increasing and Decreasing Intervals of Parabolas

Identify the vertex of a parabola from equations and graphs
Determine intervals where parabolas increase and decrease using vertex points
Analyze parabola direction using the coefficient of x² terms
Apply the vertex formula to find critical points for interval analysis
Sketch parabolas to visualize increasing and decreasing behavior
Solve real-world problems involving parabola interval analysis

Understanding Increasing and Decreasing Domain of a Parabola

Complete explanation with examples

Increasing and Decreasing Intervals of a Parabola

The intervals of increase and decrease describe the $x$ in which the parabola goes up and those in which it goes down.
Let's see it in an illustration:

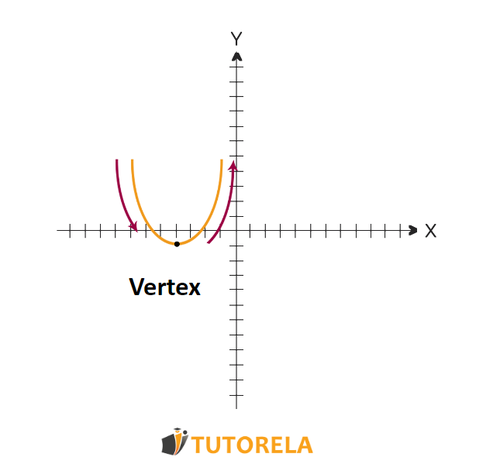
B4 - The areas of increase and decrease describe the X where the parabola increases decreases

We must always observe the function from left to right.
An increasing interval is where the function's output (y-values) gets larger as we move from left to right along the x-axis, while a decreasing interval is where the y-values get smaller as x increases.
When we see a negative slope (this is how decrease looks) – the function is decreasing.
When we see a positive slope (this is how increase looks) – the function is increasing.

The parabola will change interval only at one point - at the vertex of the parabola, he highest or lowest point of the curve. Since parabolas have a characteristic U-shape (opening upward) or upside-down U-shape (opening downward), they change from decreasing to increasing (or vice versa) at exactly once at the vertex.

Detailed explanation

Practice Increasing and Decreasing Domain of a Parabola

Test your knowledge with 58 quizzes

Based on the data in the graph

Identify the domain where the function is increasing:

Examples with solutions for Increasing and Decreasing Domain of a Parabola

Step-by-step solutions included

Exercise #1

Note that the graph of the function intersects the x-axis at points A and B

Moreover the vertex of the parabola is marked at point C

Identify the segment below where the function increases:

Step-by-Step Solution

From the graph we can see that the parabola is a smiling parabola,

meaning that its extreme point is a minimum point.

If we describe it in words, until the extreme point the function decreases,

after the extreme point it increases.

Since we measure the progress using X,

we can say that the function increases whenever X is greater than point C, the extreme point.

Mathematically we can write:

X>C

As we already said, as long as X is greater than C, the function increases.

Answer:

$x > C$

Video Solution

Exercise #2

Find the domain of increase of the function:

$y=3x^2-6x+4$

Step-by-Step Solution

The function given is $y = 3x^2 - 6x + 4$ .

First, let's find the derivative of the function, which will help us determine the intervals of increase.

The derivative is given by $f'(x) = \frac{d}{dx}(3x^2 - 6x + 4) = 6x - 6$ .

Next, find where the derivative is zero to locate critical points. Solve $6x - 6 = 0$ to get:

$6x = 6$
$x = 1$

The critical point is $x = 1$ . This is where the function changes from decreasing to increasing since quadratic functions have one axis of symmetry and $a > 0$ : indicating a parabola opening upwards.

To determine the interval of increase, analyze the sign of $f'(x)$ :

For $x > 1$ , $6x - 6 > 0$ which implies $f'(x) > 0$ , so the function is increasing.
For $x < 1$ , $6x - 6 < 0$ which implies $f'(x) < 0$ , so the function is decreasing.

Thus, the domain of increase for the function is when $x > 1$ .

The correct answer is therefore $x > 1$ .

Answer:

$x > 1$

Video Solution

Exercise #3

Find the domain of decrease of the function:

$y=-x^2+2x+35$

Step-by-Step Solution

To determine the domain over which the quadratic function $y = -x^2 + 2x + 35$ is decreasing, we proceed by identifying the vertex of the parabola.

Given the form $y = ax^2 + bx + c$ , we have $a = -1$ , $b = 2$ , and $c = 35$ . The x-coordinate of the vertex can be found using the formula:

x = -\frac{b}{2a}

Substituting $b = 2$ and $a = -1$ into the formula, we calculate:

x = -\frac{2}{2 \times (-1)} = -\frac{2}{-2} = 1

The vertex of the parabola occurs at $x = 1$ . Since the function is a downward-opening parabola (as indicated by the negative coefficient of $-x^2$ ), the function decreases for all $x$ values greater than the x-coordinate of the vertex.

Therefore, the domain of decrease for the function is $x > 1$ .

This matches the answer choice:

$x > 1$

Answer:

$x > 1$

Video Solution

Exercise #4

Find the domain of increase of the function:

$y=-x^2+2x+35$

Step-by-Step Solution

To find the domain of increase for the function $y = -x^2 + 2x + 35$ , let's determine the vertex first.

Step 1: Identify coefficients in the quadratic equation. Here, $a = -1$ , $b = 2$ , and $c = 35$ .
Step 2: Use the vertex formula $x = -\frac{b}{2a}$ to find the x-coordinate of the vertex.

Plug in the values for $b$ and $a$ :

x = -\frac{2}{2 \times -1} = -\frac{2}{-2} = 1

The x-coordinate of the vertex is $x = 1$ .

Since the coefficient $a$ is negative, this means the parabola opens downwards. A parabola opening downward will increase until it reaches the vertex, then start decreasing.

Therefore, the domain on which the function is increasing is $x < 1$ .

Therefore, the solution to the problem is $x < 1$ .

Answer:

$x < 1$

Video Solution

Exercise #5

Based on the data in the graph

Identify the domain where the function increases:

Step-by-Step Solution

Answer:

$x < 0$

Video Solution

Frequently Asked Questions

Everything you need to know about Increasing and Decreasing Domain of a Parabola

How do you find the increasing and decreasing intervals of a parabola?

To find increasing and decreasing intervals of a parabola, first locate the vertex (the turning point). For parabolas opening upward, the function decreases before the vertex and increases after it. For parabolas opening downward, the function increases before the vertex and decreases after it.

What is the vertex of a parabola and why is it important for intervals?

The vertex is the highest or lowest point of a parabola where the function changes from increasing to decreasing (or vice versa). It's the only point where a parabola changes its interval behavior, making it crucial for determining where the function goes up or down.

How do you tell if a parabola opens up or down from its equation?

Look at the coefficient of the x² term in the equation. If the coefficient is positive, the parabola opens upward (happy face). If the coefficient is negative, the parabola opens downward (sad face). This determines whether the vertex is a minimum or maximum point.

What does it mean when we say a function is increasing or decreasing?

A function is increasing when its graph goes up from left to right (positive slope). A function is decreasing when its graph goes down from left to right (negative slope). For parabolas, these intervals are separated by the vertex point.

How do you write interval notation for parabola increasing and decreasing regions?

Use the x-coordinate of the vertex as the boundary. For a parabola with vertex at x = h: if it opens upward, decreasing interval is x < h and increasing interval is x > h. Write this as (-∞, h) for decreasing and (h, ∞) for increasing.

Can a parabola be both increasing and decreasing at the same time?

No, a parabola cannot be both increasing and decreasing at the same x-value. However, a parabola has both an increasing interval and a decreasing interval, separated by the vertex. The function behavior changes exactly once at the vertex point.

What are common mistakes when finding parabola intervals?

Common mistakes include: 1) Confusing the direction of the parabola opening, 2) Not correctly identifying the vertex x-coordinate, 3) Mixing up which side of the vertex is increasing vs decreasing, 4) Forgetting that the vertex itself is neither increasing nor decreasing.

How do you find parabola intervals without a graph?

Without a graph, find the vertex using the formula x = -b/(2a) for equations in the form ax² + bx + c. Determine if the parabola opens up (a > 0) or down (a < 0). Then apply the rule: upward parabolas decrease before the vertex and increase after; downward parabolas do the opposite.

Continue Your Math Journey

Master Increasing and Decreasing Domain of a Parabola first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Vertex of a parabola Symmetry in a parabola

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Graphical representation Graphical representation with data Representation of missing b value Representation of missing c value Representation of value a only Standard representation With fractions

Parabola Increasing Decreasing Intervals Practice Problems

Understanding Increasing and Decreasing Domain of a Parabola

Increasing and Decreasing Intervals of a Parabola

Practice Increasing and Decreasing Domain of a Parabola

Examples with solutions for Increasing and Decreasing Domain of a Parabola

Frequently Asked Questions

How do you find the increasing and decreasing intervals of a parabola?

What is the vertex of a parabola and why is it important for intervals?

How do you tell if a parabola opens up or down from its equation?

What does it mean when we say a function is increasing or decreasing?

How do you write interval notation for parabola increasing and decreasing regions?

Can a parabola be both increasing and decreasing at the same time?

What are common mistakes when finding parabola intervals?

How do you find parabola intervals without a graph?

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type