Look at the circle in the diagram. AB is a chord. Is it possible to calculate the area of the circle? 5 5 5 A A A B B B

Yes, the area is $$ 12.5\pi $$cm².

Yes, the area is $$ 25\pi $$ cm².

Yes, the area is $$ 6.25\pi $$ cm².

A circle has an area of 25 cm². What is its radius? <path d="m734 384-3 12-1 1v-4q0-7-6-8h-1q-4 0-7 4-2 2-2 5t2 4h1l3 1 6 2 1 1q2 2 2 6 0 5-3 9-5 4-10 4-6 0-8-4l-3 3-1 1v-1l3-11v-1l1 1-1 3q0 6 6 7h3q4 0 7-3t3-6q0-4-4-5h-1l-6-2q-3-1-4-4l-1-3q0-5 4-8 4-4 9-4t7 4l2-3 1-1h1Zm50 19h-30l-2-1 2-1h30l2 1-2 1m0 10h-30l-2-1 2-1h30l2 1-2 1Zm42-2-1 9h-19v-2l10-11q5-6 5-11t-2-7l-4-2q-4 0-6 4l-1 2 3 1v1q0 2-2 3h-1l-2-2v-1q0-4 3-7 2-2 6-2 6 0 9 4 2 2 2 5v1q0 3-3 7l-4 4-3 3-1 1-5 5h9l5-1 1-4h1Zm26-1q0 5-4 8-3 3-7 3-5 0-8-4-2-2-2-5t2-3h1q2 0 2 2l-1 3h-2q1 3 4 5l3 1q4 0 6-4l1-7-1-6q-1-3-4-3-4 0-7 3v1l-1-1v-17h1l7 1 7-1h1l-2 3q-3 3-8 3l-5-1v10q3-3 7-3t7 4q3 3 3 8Z" paint-order="stroke fill markers">

$$ \frac{2.5}{\sqrt{\pi}} $$ cm

Circle Practice Problems - Circumference, Area & Elements

Master circle geometry with practice problems on circumference, area, radius, diameter, and arc calculations. Step-by-step solutions included.

📚Master Circle Geometry Through Interactive Practice

Calculate circumference using the formula P = 2πr with various radius values
Find circle area using A = πr² for whole circles and semicircles
Convert between radius and diameter measurements in circle problems
Identify and work with circle elements: radius, diameter, chord, arc, and tangent
Solve real-world problems involving circular shapes and measurements
Apply the Pythagorean theorem to find missing circle dimensions

Understanding Circle

Complete explanation with examples

Elements of the circumference

What is circumference?

This question is not easy to answer and even more complicated to understand. If you imagine any point on a flat surface and a series of points whose distance from that point is identical, then you are looking at a circle.

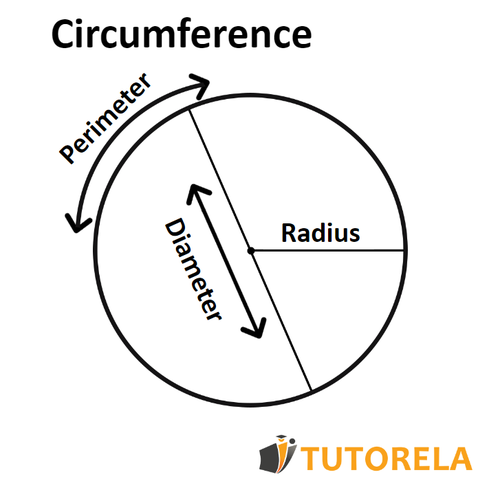
A circumference is the boundary of a circle, and its elements include:

Radius: The distance from the center of the circle to any point on the circumference.
Diameter: A straight line passing through the center that connects two points on the circumference, equal to twice the radius.
Arc: A portion of the circumference.
Chord: A line segment connecting two points on the circle.
Tangent: A line that touches the circle at exactly one point.

Detailed explanation

Practice Circle

Test your knowledge with 60 quizzes

A circle has a circumference of 31.41.

What is its radius?

Examples with solutions for Circle

Step-by-step solutions included

Exercise #1

Look at the circle in the figure:

Its radius is equal to 4.

What is its circumference?

Step-by-Step Solution

The formula for the circumference is equal to:

$2\pi r$

Answer:

8π

Video Solution

Exercise #2

Look at the circle in the figure:

The radius is equal to 7.

What is the area of the circle?

Step-by-Step Solution

Remember that the formula for the area of a circle is

πR²

We replace the data we know:

π7²

π49

Answer:

49π

Video Solution

Exercise #3

O is the center of the circle in the figure below.

What is its circumference?

Step-by-Step Solution

We use the formula: $P=2\pi r$

We replace the data in the formula: $P=2\times8\pi$

$P=16\pi$

Answer:

$16\pi$ cm

Video Solution

Exercise #4

Given that the diameter of the circle is 7 cm

What is the area?

Step-by-Step Solution

First we need the formula for the area of a circle:

$\pi r^2$

In the question, we are given the diameter of the circle, but we still need the radius.

It is known that the radius is actually half of the diameter, therefore:

$r=7:2=3.5$

We substitute the value into the formula.

$\pi3.5^2=12.25\pi$

Answer:

$12.25\pi$ cm².

Video Solution

Exercise #5

O is the center of the circle in the diagram below.

What is its area?

Step-by-Step Solution

Remember that the formula for the area of a circle is

πR²

We insert the known data:

π3²

π9

Answer:

$9\pi$ cm²

Video Solution

Frequently Asked Questions

Everything you need to know about Circle

What is the formula for finding the circumference of a circle?

The circumference formula is P = 2πr, where P is the perimeter, π (pi) equals approximately 3.14, and r is the radius. You can also use P = πd where d is the diameter, since diameter equals twice the radius.

How do you calculate the area of a circle step by step?

To find circle area: 1) Identify the radius length, 2) Square the radius (multiply it by itself), 3) Multiply the result by π (3.14). The formula is A = πr². For example, if radius = 5, then A = π × 5² = π × 25 = 78.5 square units.

What's the difference between radius and diameter in a circle?

The radius is the distance from the center to any point on the circle's edge. The diameter is a straight line passing through the center, connecting two points on the circle. The diameter is always exactly twice the radius length.

How do you find the radius when given the diameter?

To find the radius from diameter, simply divide the diameter by 2. Since diameter = 2 × radius, then radius = diameter ÷ 2. For example, if diameter = 20 cm, then radius = 20 ÷ 2 = 10 cm.

What are the main elements of a circle I need to know?

The key circle elements are: • Radius: distance from center to edge • Diameter: line through center connecting two edge points • Circumference: the boundary or perimeter of the circle • Arc: a portion of the circumference • Chord: line segment connecting two points on the circle • Tangent: line touching the circle at exactly one point

How do you calculate the area of a semicircle?

For semicircle area, first calculate the full circle area using A = πr², then divide by 2. For example, if radius = 7, full circle area = π × 7² = 49π, so semicircle area = 49π ÷ 2 = 24.5π square units.

What is pi (π) and why is it important in circle calculations?

Pi (π) is a mathematical constant approximately equal to 3.14159, representing the ratio of any circle's circumference to its diameter. It's essential for all circle calculations involving circumference and area, appearing in formulas like P = 2πr and A = πr².

Common mistakes students make when solving circle problems?

Typical errors include: 1) Confusing radius with diameter in formulas, 2) Forgetting to square the radius in area calculations, 3) Using wrong units in final answers, 4) Not converting between radius and diameter when needed. Always double-check which measurement you have and which formula requires.

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Applying the formula A shape consisting of several shapes (requiring the same formula) Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Applying the formula Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Impact of a radius change on the area of a circle Increasing a specific element by addition of.....or multiplication by....... Subtraction or addition to a larger shape Using additional geometric shapes Using Pythagoras' theorem Applying the formula A shape consisting of several shapes (requiring the same formula) Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Calculate by how much the perimeter has increased Calculating arc length Identifying and defining elements Identify the greater value Increasing a specific element by addition of.....or multiplication by....... Subtraction or addition to a larger shape Using additional geometric shapes Using Pythagoras' theorem Using variables Verifying whether or not the formula is applicable Worded problems

Circle Practice Problems - Circumference, Area & Elements

Understanding Circle

Elements of the circumference

What is circumference?

Practice Circle

Examples with solutions for Circle

Frequently Asked Questions

What is the formula for finding the circumference of a circle?

How do you calculate the area of a circle step by step?

What's the difference between radius and diameter in a circle?

How do you find the radius when given the diameter?

What are the main elements of a circle I need to know?

How do you calculate the area of a semicircle?

What is pi (π) and why is it important in circle calculations?

Common mistakes students make when solving circle problems?

More Circle Questions

Circle

Circumference

Area of a Circle for ninth grade

Area of a Circle

Practice by Question Type

More Resources and Links