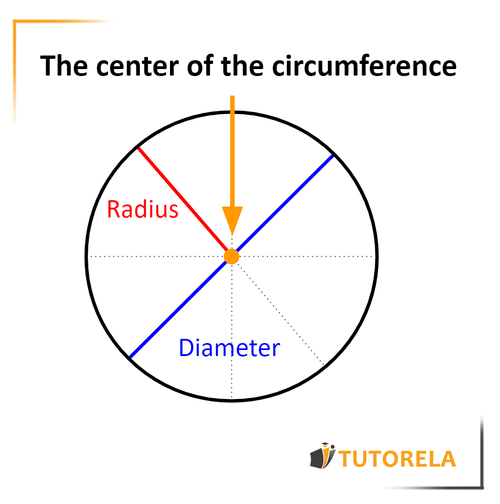
The Center of a Circle - Examples, Exercises and Solutions

The center of the circumference belongs to subtopics that make up the topic of the circumference and the circle. We use the concept of the center of the circumference to define the circumference itself, as well as to calculate the radius and diameter of each given circumference.

The center of the circumference, as its name indicates, is a point located in the center of the circumference. It is usually customary to mark this point with the letter O. Indeed, this point is at the same distance from each of the points that make up the circumference.

Detailed explanation

Practice The Center of a Circle

Question 1

There are only 4 radii in a circle.

Question 2

Is there sufficient data to determine that

$$ GH=AB $$

Question 3

M is the center of the circle.

Perhaps $$ AB=CD $$

Question 4

In which of the circles is the center of the circle marked?

Question 5

M is the center of the circle.

Perhaps $$ MF=MC $$

examples with solutions for the center of a circle

Exercise #1

There are only 4 radii in a circle.

Step-by-Step Solution

A radius is a straight line that connects the center of the circle with a point on the circle itself.

Therefore, the answer is incorrect, as there are infinite radii.

Answer

False

Exercise #2

Is there sufficient data to determine that

$GH=AB$

Video Solution

Answer

Exercise #3

M is the center of the circle.

Perhaps $AB=CD$

Video Solution

Answer

Exercise #4

In which of the circles is the center of the circle marked?

Video Solution

Answer

Exercise #5

M is the center of the circle.

Perhaps $MF=MC$

Video Solution

Answer

Yes

Question 1

M is the center of the circle.

In the figure we observe 3 diameters?

Question 2

M is the center of the circle below.

$$ AB=10 $$

Can a chord with a length of 15 cm be drawn in the circle?

Question 3

M is the center of the circle shown below.

AB is a chord in the circle and is 8 long.

Which of the options is a reasonable length for circle's diameter?

Question 4

Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?

Question 5

M is the center of the circle.

Perhaps $$ CM+MD=2EM $$