A circle has an area of 25 cm². What is its radius? <path d="m734 384-3 12-1 1v-4q0-7-6-8h-1q-4 0-7 4-2 2-2 5t2 4h1l3 1 6 2 1 1q2 2 2 6 0 5-3 9-5 4-10 4-6 0-8-4l-3 3-1 1v-1l3-11v-1l1 1-1 3q0 6 6 7h3q4 0 7-3t3-6q0-4-4-5h-1l-6-2q-3-1-4-4l-1-3q0-5 4-8 4-4 9-4t7 4l2-3 1-1h1Zm50 19h-30l-2-1 2-1h30l2 1-2 1m0 10h-30l-2-1 2-1h30l2 1-2 1Zm42-2-1 9h-19v-2l10-11q5-6 5-11t-2-7l-4-2q-4 0-6 4l-1 2 3 1v1q0 2-2 3h-1l-2-2v-1q0-4 3-7 2-2 6-2 6 0 9 4 2 2 2 5v1q0 3-3 7l-4 4-3 3-1 1-5 5h9l5-1 1-4h1Zm26-1q0 5-4 8-3 3-7 3-5 0-8-4-2-2-2-5t2-3h1q2 0 2 2l-1 3h-2q1 3 4 5l3 1q4 0 6-4l1-7-1-6q-1-3-4-3-4 0-7 3v1l-1-1v-17h1l7 1 7-1h1l-2 3q-3 3-8 3l-5-1v10q3-3 7-3t7 4q3 3 3 8Z" paint-order="stroke fill markers">

$$ \frac{2.5}{\sqrt{\pi}} $$ cm

What is the area of the flower represented in the diagram? 2x 3 2 1.2x 1.5x

$$ 4x^2\pi+13\pi+3.69\pi x^2 $$

Given a circle whose center O. From the center of the circle go out 2 radii that cut the circle at the points A and B. Given AO⊥OB. The side AB is equal to and+2. Express band and the area of the circle. y+2 y+2 y+2 A A A B B B O O O

$$ \frac{\pi}{\sqrt{2}}\frac{}{}\lbrack y^2+4] $$

$$ \frac{\pi}{\sqrt{2}}[y^2+4y+4] $$

Area of a Circle Practice Problems and Worksheets

Master circle area calculations with step-by-step practice problems. Learn to find area using radius, diameter, and reverse calculations with detailed solutions.

📚Master Circle Area Calculations with Interactive Practice

Calculate circle area using the formula A = π × R² with given radius values
Convert diameter to radius and solve for circle area step-by-step
Find radius when given the area of a circle using reverse calculations
Apply area formulas to real-world circle problems with visual diagrams
Practice with mixed problems involving both radius and diameter measurements
Solve complex circle area word problems with detailed solution explanations

Understanding Area of a Circle

Complete explanation with examples

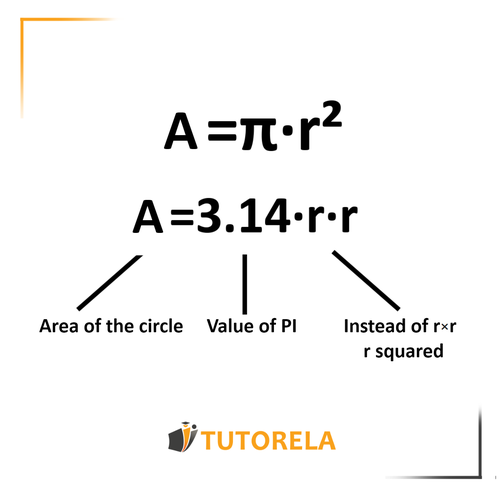
The area of the circle is, in fact, the surface that is "enclosed" within the perimeter of the circumference. It is calculated by raising the radius of the circumference $R$ to the second power and multiplying the result by -> $π$ . The area of the circle is usually denoted by the letter $A$ .

The formula to calculate the area of a circle is:

$A=\pi\times R\times R$

$A$ -> area of the circle
$\pi–>PI=3.14$
$R$ -> Radius of the circumference

In problems that include the radius - We will use the radius in the formula.
In problems that include the diameter - We will divide it by $2$ to obtain the radius and, only then, place the radius in the formula.
In problems that include the area and ask to find the radius - We will place the area in the formula and find the radius.

A1 - The formula to calculate the area of a circle

$A=π\times R\times R$

Detailed explanation

Practice Area of a Circle

Test your knowledge with 23 quizzes

What is the area of the flower represented in the diagram?

Examples with solutions for Area of a Circle

Step-by-step solutions included

Exercise #1

Given that the diameter of the circle is 7 cm

What is the area?

Step-by-Step Solution

First we need the formula for the area of a circle:

$\pi r^2$

In the question, we are given the diameter of the circle, but we still need the radius.

It is known that the radius is actually half of the diameter, therefore:

$r=7:2=3.5$

We substitute the value into the formula.

$\pi3.5^2=12.25\pi$

Answer:

$12.25\pi$ cm².

Video Solution

Exercise #2

O is the center of the circle in the diagram below.

What is its area?

Step-by-Step Solution

Remember that the formula for the area of a circle is

πR²

We insert the known data:

π3²

π9

Answer:

$9\pi$ cm²

Video Solution

Exercise #3

Look at the circle in the figure:

The radius is equal to 7.

What is the area of the circle?

Step-by-Step Solution

Remember that the formula for the area of a circle is

πR²

We replace the data we know:

π7²

π49

Answer:

49π

Video Solution

Exercise #4

A circle has an area of 25 cm².

What is its radius?

Step-by-Step Solution

Area of the circle:

$S=\pi r^2$

We insert the known data:

$25=\pi r^2$

Divide by Pi: $\frac{25}{\pi}=r^2$

Extract the root: $\sqrt{\frac{25}{\pi}}=r$

$\frac{5}{\sqrt{\pi}}=r$

Answer:

$\frac{5}{\sqrt{\pi}}$ cm

Video Solution

Exercise #5

Look at the circle in the diagram.

AB is a chord.

Is it possible to calculate the area of the circle?

Step-by-Step Solution

Since AB is just a chord and we know nothing else about the diameter or the radius, we cannot calculate the area of the circle.

Answer:

It is not possible.

Video Solution

Frequently Asked Questions

Everything you need to know about Area of a Circle

What is the formula for finding the area of a circle?

The formula for the area of a circle is A = π × R², where A is the area, π (pi) equals approximately 3.14, and R is the radius. You can also write this as A = π × R × R if you're not comfortable with exponents.

How do I find the area of a circle when given the diameter?

When given the diameter, first divide it by 2 to get the radius (since diameter = 2 × radius). Then use the area formula A = π × R² with your calculated radius value.

What steps should I follow to solve circle area problems?

Follow these steps: 1) Identify if you have radius or diameter, 2) Convert diameter to radius if needed (divide by 2), 3) Substitute values into A = π × R², 4) Calculate R² first, 5) Multiply by π (3.14), 6) Include proper units (cm², m², etc.).

How do I find the radius when I know the area of a circle?

To find radius from area, use the formula A = π × R² and solve for R. Divide the area by π (3.14), then take the square root of the result to get the radius.

What are common mistakes when calculating circle area?

Common mistakes include: forgetting to square the radius, using diameter instead of radius in the formula, not converting units properly, and forgetting to include area units (like cm² or m²) in the final answer.

Why do we use π (pi) in the circle area formula?

Pi (π ≈ 3.14) represents the mathematical constant that relates a circle's circumference to its diameter. It appears in the area formula because the area calculation is derived from the geometric properties of circles.

What units should I use for circle area answers?

Circle area is always expressed in square units such as cm², m², ft², or in². The unit depends on what unit was used for the radius or diameter measurement in the original problem.

Can I use 3.14 instead of the π symbol in calculations?

Yes, you can use 3.14 as an approximation for π in most basic calculations. For more precise answers, you might use 3.14159 or leave your answer in terms of π (like 25π cm²).

Continue Your Math Journey

Master Area of a Circle first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

Area Elements of the circumference

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems

Applying the formula A shape consisting of several shapes (requiring the same formula) Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Applying the formula Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Impact of a radius change on the area of a circle Increasing a specific element by addition of.....or multiplication by....... Subtraction or addition to a larger shape Using additional geometric shapes Using Pythagoras' theorem

Area of a Circle Practice Problems and Worksheets

Understanding Area of a Circle

Practice Area of a Circle

Examples with solutions for Area of a Circle

Frequently Asked Questions

What is the formula for finding the area of a circle?

How do I find the area of a circle when given the diameter?

What steps should I follow to solve circle area problems?

How do I find the radius when I know the area of a circle?

What are common mistakes when calculating circle area?

Why do we use π (pi) in the circle area formula?

What units should I use for circle area answers?

Can I use 3.14 instead of the π symbol in calculations?

Continue Your Math Journey

Suggested Topics to Practice in Advance

Topics Learned in Later Sections

Practice by Question Type