Circumference Practice Problems - Circle Perimeter Worksheets

Master circumference calculations with step-by-step practice problems. Learn to find circle perimeter using radius and diameter formulas with detailed solutions.

📚What You'll Master in This Circumference Practice
  • Calculate circumference using the formula P = 2πr with given radius values
  • Find circle perimeter when diameter is provided using P = πd formula
  • Solve reverse problems to find radius or diameter from given circumference
  • Apply circumference concepts to real-world scenarios like bicycle wheels and tracks
  • Work with both exact answers (in terms of π) and decimal approximations
  • Analyze complex shapes involving quarter circles and combined figures

Understanding Circumference

Complete explanation with examples

The circumference is actually the length of the circular line. It is calculated by multiplying the radius by 2, which has an approximate value of π. It can also be said that the circumference is equal to the the diameter of the circumference multiplied by π (since the diameter is actually twice the radius of the circumference). It is customary to identify the circumference (the perimeter) with the letter P.

The formula for calculating the circumference is:

P=2×π×R P=2\times\pi\times R

We will illustrate the concept with a simple example. Here is a circle, as shown in the drawing in front of you:

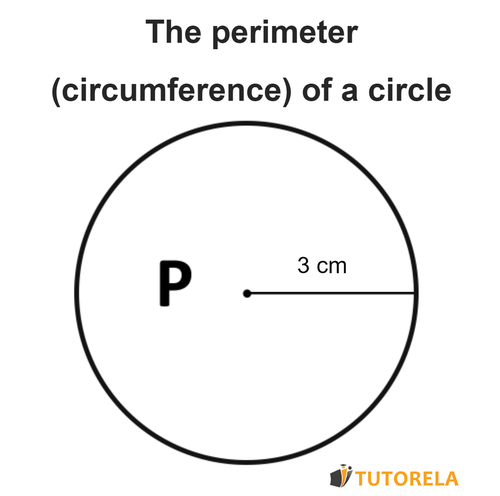
C - perimeter of the circumference

The radius of the circumference is 3 cm 3\text{ cm} .

You can calculate the circumference of the circle by placing the data:

P=2×R×π=2×3×3.14=18.84 P=2\times R\timesπ=2\times3\times3.14=18.84

That is, the circumference is 18.84 cm 18.84\text{ cm} .

Detailed explanation

Practice Circumference

Test your knowledge with 30 quizzes

Below is a circle bounded by a parallelogram:

36

All meeting points are tangential to the circle.
The circumference is 25.13.

What is the area of the parallelogram?

Examples with solutions for Circumference

Step-by-step solutions included
Exercise #1

O is the center of the circle in the figure below.

888OOO What is its circumference?

Step-by-Step Solution

We use the formula:P=2πr P=2\pi r

We replace the data in the formula:P=2×8π P=2\times8\pi

P=16π P=16\pi

Answer:

16π 16\pi cm

Video Solution
Exercise #2

Look at the circle in the figure:

444

Its radius is equal to 4.

What is its circumference?

Step-by-Step Solution

The formula for the circumference is equal to:

2πr 2\pi r

Answer:

8π

Video Solution
Exercise #3

Look at the circle in the figure.

What is its circumference if its radius is equal to 6?

6

Step-by-Step Solution

Formula of the circumference:

P=2πr P=2\pi r

We insert the given data into the formula:

P=2×6×π P=2\times6\times\pi

P=12π P=12\pi

Answer:

12π 12\pi

Video Solution
Exercise #4

Is it possible that the circumference of a circle is 8 meters and its diameter is 4 meters?

Step-by-Step Solution

To calculate, we will use the formula:

P2r=π \frac{P}{2r}=\pi

Pi is the ratio between the circumference of the circle and the diameter of the circle.

The diameter is equal to 2 radii.

Let's substitute the given data into the formula:

84=π \frac{8}{4}=\pi

2≠π 2\ne\pi

Therefore, this situation is not possible.

Answer:

Impossible

Video Solution
Exercise #5

Look at the circle in the figure.

The radius of the circle is 23 \frac{2}{3} .

What is its perimeter?

Step-by-Step Solution

The radius is a straight line that extends from the center of the circle to its outer edge.

The radius is essential for calculating the circumference of the circle, which can be found using the following formula:

If we substitute in the radius we have, the formula will be:

2*π*2/3

To solve this, first we'll rearrange the formula like so:

π*2*2/3 =

We'll then multiply the fraction by the whole number:

π*(2*2)/3 =

π*4/3 =

4/3π

Answer:

43π \frac{4}{3}\pi

Video Solution

Frequently Asked Questions

Everything you need to know about Circumference

What is the formula for calculating circumference?

+
The circumference formula is P = 2πr, where P is the perimeter, π ≈ 3.14, and r is the radius. You can also use P = πd when the diameter is given, since diameter equals twice the radius.

How do I find circumference when only the radius is given?

+
Simply substitute the radius value into the formula P = 2πr. For example, if r = 5 cm, then P = 2 × π × 5 = 10π cm ≈ 31.4 cm.

What's the difference between circumference and diameter?

+
Circumference is the complete distance around a circle (the perimeter), while diameter is the straight line distance across the circle through its center. The circumference is always π times longer than the diameter.

Can I find the radius if I know the circumference?

+
Yes! Rearrange the formula P = 2πr to solve for r: r = P/(2π). Divide the circumference by 2π to get the radius.

Why do we use π in circumference calculations?

+
Pi (π) represents the constant ratio between any circle's circumference and its diameter. This ratio is approximately 3.14159, which means every circle's circumference is about 3.14 times its diameter.

What are common real-world applications of circumference?

+
Circumference calculations are used for: 1) Determining wheel distances traveled, 2) Calculating material needed for circular borders, 3) Finding track lengths for circular paths, 4) Designing circular objects and structures.

Should I leave answers in terms of π or convert to decimals?

+
This depends on the problem requirements. Exact answers use π (like 6π cm), while approximate answers use decimals (like 18.84 cm). Exact answers are more precise for further calculations.

How do I solve circumference problems with variables?

+
Treat variables like regular numbers in the formula. For example, if circumference is 9aπ cm, then r = 9aπ/(2π) = 4.5a cm. The variable remains part of your final answer.

Continue Your Math Journey

Master Circumference first, then advance to these related topics that build on your fraction skills

Topics Learned in Later Sections

CircleDiameterPiThe Center of a CircleRadiusHow is the radius calculated using its circumference?PerimeterParts of a CircleAreaElements of the circumferenceArea of a circle

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Applying the formula A shape consisting of several shapes (requiring the same formula) Calculate The Missing Side based on the formula Calculating parts of the circle Finding Area based off Perimeter and Vice Versa Calculate by how much the perimeter has increased Calculating arc length Identifying and defining elements Identify the greater value Increasing a specific element by addition of.....or multiplication by....... Subtraction or addition to a larger shape Using additional geometric shapes Using Pythagoras' theorem Using variables Verifying whether or not the formula is applicable Worded problems