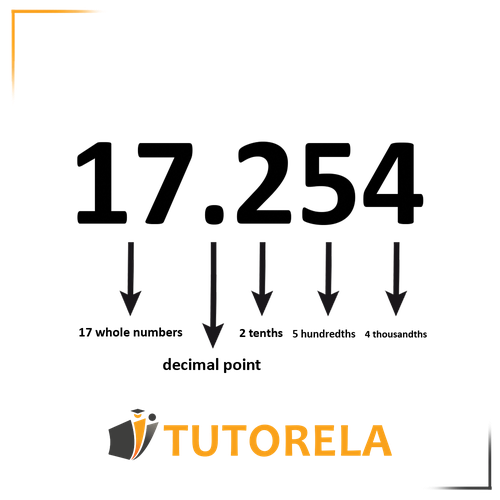
Converting a decimal fraction to a mixed number - Examples, Exercises and Solutions

Converting a decimal to a mixed number

To convert a decimal fraction to a mixed fraction,
we ask ourselves how to read the decimal fraction or in other words, what the last digit represents –
if we use the word tenths – we place 10 in the denominator
if we use the word hundredths – we place 100 in the denominator
if we use the word thousandths – we place 1000 in the denominator

The number itself – everything that appears after the decimal point, we place in the numerator.
The whole number in the decimal fraction, we add to the mixed fraction as the whole number in the mixed fraction.

Detailed explanation

Practice Converting a decimal fraction to a mixed number

Question 1

Write the following fraction as a decimal:

$\frac{7}{10}=$

Question 2

Write the following fraction as a decimal:

$\frac{5}{10}=$

Question 3

$$ 0.171= $$

Question 4

Write the following fraction as a decimal:

$\frac{1}{100}=$

Question 5

Write the following fraction as a decimal:

$\frac{20}{100}=$

examples with solutions for converting a decimal fraction to a mixed number

Exercise #1

Write the following fraction as a decimal:

$\frac{7}{10}=$

Video Solution

Step-by-Step Solution

Write the simple fraction in decimal form

$7.0$

Since the fraction is divisible by 10, move the decimal point one place to the left and get:

$.7$

Let's add the zero to the left of the decimal point and get:

$0.7$

Answer

0.7

Exercise #2

Write the following fraction as a decimal:

$\frac{5}{10}=$

Video Solution

Step-by-Step Solution

Write the simple fraction in decimal form

$5.0$

Since the fraction is divided by 10, move the decimal point one place to the left and get:

$.5$

Complete the zero to the left of the decimal point and get:

$0.5$

Answer

0.5

Exercise #3

$0.171=$

Video Solution

Step-by-Step Solution

Let's pay attention to where the decimal point is located in the number.

Remember:

One number after the decimal point represents tenths

Two numbers after the decimal point represent hundredths

Three numbers after the decimal point represent thousandths

And so on

In this case there are three numbers after the decimal point so the number is divided by 1000

Write the fraction in the following way:

$\frac{0171}{1000}$

We will remove the extra zeros and get:

$\frac{171}{1000}$

Answer

$\frac{171}{1000}$

Exercise #4

Write the following fraction as a decimal:

$\frac{1}{100}=$

Video Solution

Answer

0.01

Exercise #5

Write the following fraction as a decimal:

$\frac{20}{100}=$

Video Solution

Answer

0.2

Question 1

Write the following fraction as a decimal:

$\frac{3}{100}=$

Question 2

Write the following fraction as a decimal:

$\frac{11}{100}=$

Question 3

Write the following fraction as a decimal:

$\frac{5}{100}=$

Question 4

Write the following fraction as a decimal:

$\frac{53}{100}=$

Question 5

Write the following fraction as a decimal:

$\frac{47}{100}=$