So how do we convert a simple fraction to a decimal fraction? First, we can reassure you by saying that the answer is: quite easily. All you need is to understand the technique, and mainly to understand the meaning of the decimal fraction. First, what do decimal fractions look like? They appear in the following form: 0.5, 3.6, and so on. Or in other words: "the fraction with the point".
Converting Decimals to Fractions Practice Problems
Master converting decimal numbers to simple fractions and mixed numbers with step-by-step practice problems, interactive exercises, and detailed solutions.
📚What You'll Master in This Practice Session
- Convert decimal numbers like 0.5, 0.25, and 0.125 to simple fractions
- Transform decimals with denominators of 10, 100, and 1000 into fraction form
- Simplify decimal fractions to their lowest terms using greatest common factors
- Convert improper decimal fractions to mixed numbers with whole parts
- Identify the relationship between decimal places and fraction denominators
- Apply conversion techniques to solve real-world decimal-to-fraction problems
Understanding Converting Decimal Fractions to Simple Fractions and Mixed Numbers
Complete explanation with examples
Converting a simple fraction to decimal - how to calculate?
In fact, there is a point that creates the boundary between the whole number and the fraction. To convert a simple fraction to a decimal fraction, you need to choose a denominator: 10, 100, or 1000. So how can you also convert "simple" fractions to decimal fractions? Pay attention:
Basic fraction data:
- The line that separates between two different numbers is called the fraction line.
- The top part of the fraction - numerator.
- The bottom part of the fraction - denominator.
Note that when we convert a "classic" simple fraction to a decimal fraction, the fraction line disappears, and a decimal point separates the numbers.
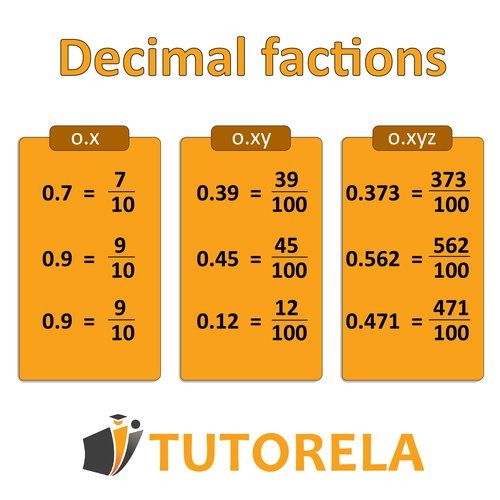
Practice Converting Decimal Fractions to Simple Fractions and Mixed Numbers
Test your knowledge with 58 quizzes
Write the following fraction as a decimal:
\( \frac{50}{100}= \)
Examples with solutions for Converting Decimal Fractions to Simple Fractions and Mixed Numbers
Step-by-step solutions included
Exercise #1
Write the following fraction as a decimal:
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we'll move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer:
0.05
Video Solution
Exercise #2
Write the following fraction as a decimal:
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer:
0.03
Video Solution
Exercise #3
Write the following fraction as a decimal:
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer:
0.03
Video Solution
Exercise #4
Write the following fraction as a decimal:
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer:
0.11
Video Solution
Exercise #5
Write the following fraction as a decimal:
Step-by-Step Solution
Let's write the simple fraction as a decimal fraction
Since the fraction divides by 100, we move the decimal point once to the left and get:
We'll add the zero before the decimal point and get:
Answer:
0.19
Video Solution
Frequently Asked Questions
How do you convert 0.25 to a fraction step by step?
+To convert 0.25 to a fraction: 1) Write 25/100 (25 over 100), 2) Find the GCD of 25 and 100, which is 25, 3) Divide both numerator and denominator by 25 to get 1/4. The decimal 0.25 equals the fraction 1/4.
What's the easiest way to convert decimals to fractions?
+The easiest method is to use the decimal place value as your denominator. One decimal place uses 10, two decimal places use 100, three use 1000, and so on. Then simplify the resulting fraction by dividing both parts by their greatest common divisor.
How do you convert 0.125 to a simple fraction?
+Since 0.125 has three decimal places, write it as 125/1000. Then simplify by dividing both numerator and denominator by their GCD (125): 125÷125 = 1 and 1000÷125 = 8, giving you 1/8.
What fraction equals 0.75 in simplest form?
+0.75 equals 75/100. To simplify, find the GCD of 75 and 100, which is 25. Divide both by 25: 75÷25 = 3 and 100÷25 = 4. Therefore, 0.75 = 3/4 in simplest form.
How do you convert repeating decimals like 0.333... to fractions?
+For repeating decimals, use algebraic methods. Let x = 0.333..., then 10x = 3.333.... Subtract the first equation from the second: 9x = 3, so x = 3/9 = 1/3. Therefore, 0.333... = 1/3.
When should you convert a decimal to a mixed number instead of a simple fraction?
+Convert to a mixed number when the decimal is greater than 1, like 2.75. First convert the decimal part (0.75 = 3/4), then combine with the whole number to get 2 3/4. Mixed numbers are often easier to visualize and understand than improper fractions.
What's the difference between 0.5 as a fraction and 0.05 as a fraction?
+0.5 has one decimal place, so it becomes 5/10 = 1/2. 0.05 has two decimal places, so it becomes 5/100 = 1/20. The key difference is the number of decimal places, which determines the denominator (10 vs 100).
How do you check if your decimal to fraction conversion is correct?
+Divide the numerator by the denominator using long division or a calculator. The result should equal your original decimal. For example, to verify 3/4 = 0.75, divide 3÷4 = 0.75. If the results match, your conversion is correct.