Solve the following problem:
2x+7−5x−12=−8x+3
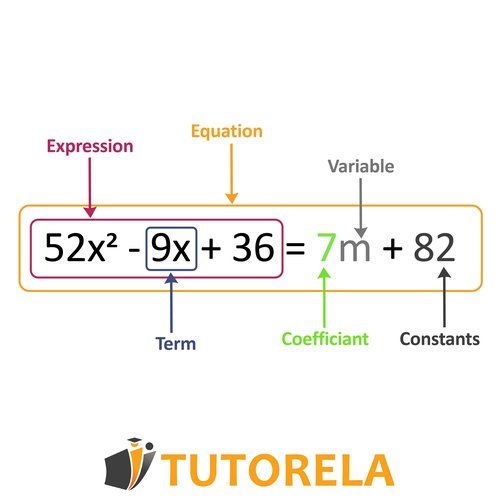
In order to solve this exercise, we first need to identify that we have an equation with an unknown.
To solve such equations, the first step will be to arrange the equation so that on one side we have the numbers and on the other side the unknowns.
2X+7−5X−12=−8X+3
First, we'll move all unknowns to one side.
It's important to remember that when moving terms, the sign of the number changes (from negative to positive or vice versa).
2X+7−5X−12+8X=3
Now we'll do the same thing with the regular numbers.
2X−5X+8X=3−7+12
In the next step, we'll calculate the numbers according to the addition and subtraction signs.
2X−5X=−3X
−3X+8X=5X
3−7=−4
−4+12=8
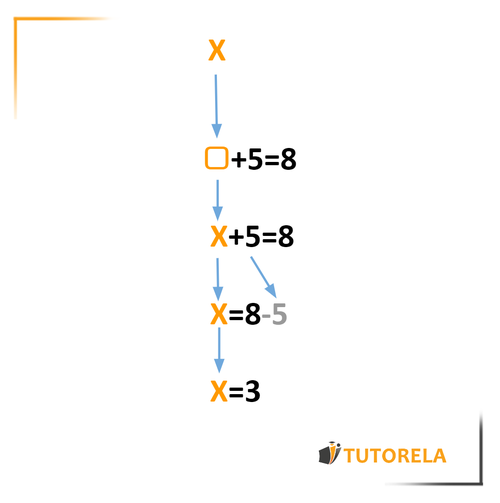
5X=8
At this stage, we want to reach a state where we have only one X, not 5X,
Thus we'll divide both sides of the equation by the coefficient of the unknown (in this case - 5).
X=58