Before going deeper into opposite angles, we will pause a moment to visualize the types of scenarios where this type of angle can be found. To make it easier to understand, we will draw two parallel straight lines cut by a secant or transversal, as shown in the following illustration:
Vertically Opposite Angles - Examples, Exercises and Solutions
Understanding Vertically Opposite Angles
Complete explanation with examples
What are opposite angles?
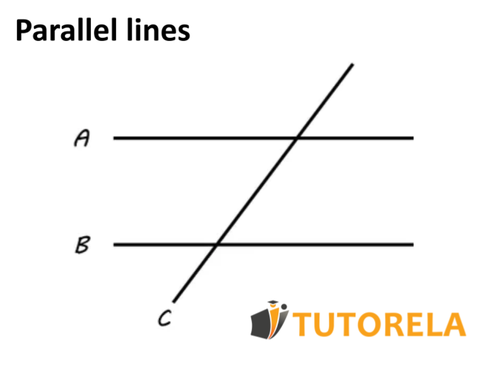
What do we see here? The transversal intersects with each one of the straight lines and (in our case and are parallel, although this is not required in order to get opposite angles).
With this example in mind, we are ready to move on to the formal definition of opposite angles, which will help us to identify them more easily:
Opposite angles are a pair of angles that arise when two straight lines intersect. These angles are formed at the point of intersection (which we will call the vertex), one in front of the other. Opposite angles are equal.
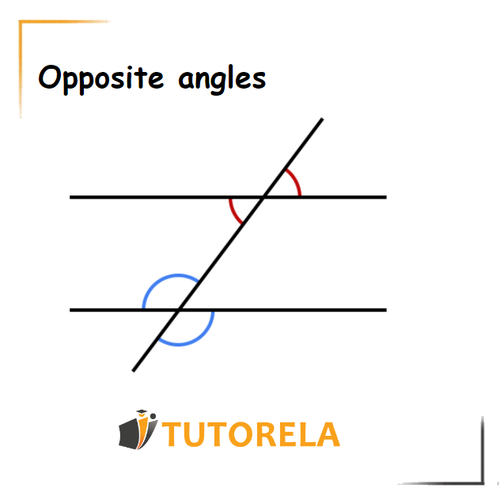
In the following illustration, we can see two examples of opposite angles, the first pair is marked in red and the second pair in blue.
Practice Vertically Opposite Angles
Test your knowledge with 48 quizzes
Does the diagram show an adjacent angle?
Examples with solutions for Vertically Opposite Angles
Step-by-step solutions included
Exercise #1
Identify the angle shown in the figure below?
Step-by-Step Solution
Remember that adjacent angles are angles that are formed when two lines intersect one another.
These angles are created at the point of intersection, one adjacent to the other, and that's where their name comes from.
Adjacent angles always complement one another to one hundred and eighty degrees, meaning their sum is 180 degrees.
Answer:
Adjacent
Exercise #2
Identify the angles shown in the diagram below?
Step-by-Step Solution
Let's remember that vertical angles are angles that are formed when two lines intersect. They are are created at the point of intersection and are opposite each other.
Answer:
Vertical
Exercise #3
Which type of angles are shown in the figure below?
Step-by-Step Solution
Alternate angles are a pair of angles that can be found on the opposite side of a line that cuts two parallel lines.
Furthermore, these angles are located on the opposite level of the corresponding line that they belong to.
Answer:
Alternate
Exercise #4
Which type of angles are shown in the diagram?
Step-by-Step Solution
First let's remember that corresponding angles can be defined as a pair of angles that can be found on the same side of a transversal line that intersects two parallel lines.
Additionally, these angles are positioned at the same level relative to the parallel line to which they belong.
Answer:
Corresponding
Exercise #5
is parallel to
Determine which of the statements is correct.
Step-by-Step Solution
Let's review the definition of adjacent angles:
Adjacent angles are angles formed where there are two straight lines that intersect. These angles are formed at the point where the intersection occurs, one next to the other, and hence their name.
Now let's review the definition of collateral angles:
Two angles formed when two or more parallel lines are intersected by a third line. The collateral angles are on the same side of the intersecting line and even are at different heights in relation to the parallel line to which they are adjacent.
Therefore, answer C is correct for this definition.
Answer:
Colaterales Adjacent
Video Solution