Angles in Parallel Lines Practice Problems & Solutions

Master corresponding angles, alternate angles, and co-interior angles with step-by-step practice problems. Perfect for grades 7-10 geometry students.

📚What You'll Master in This Practice Session
  • Identify corresponding angles when parallel lines are cut by a transversal
  • Calculate alternate interior and exterior angles using angle relationships
  • Solve for unknown angles using co-interior angle properties
  • Apply angle theorems to solve multi-step geometry problems
  • Recognize and use vertically opposite angles in parallel line diagrams
  • Master proof techniques for parallel line angle relationships

Understanding Alternate angles

Complete explanation with examples

Alternate angles

Definition:

Alternate angles are on opposite sides of the transversal that intersects two parallel lines and are not on the same side of the parallel lines to which they belong.
Alternate angles are equal.

The following sketch illustrates two pairs of alternate angles, one is painted red and the other blue.

two pairs of alternate angles, one is painted red and the other blue.

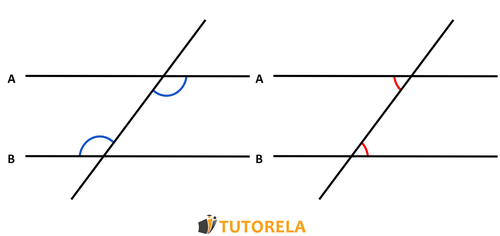
Identifying Alternate Angles:

There are two types of alternate angles: alternate interior (inside the parallel lines) and alternate exterior (outside the parallel lines). These angles are always equal when the lines are parallel.

The Significance of Parallel Lines:

For alternate angles to be congruent, the lines must be parallel. Recognizing this can help in solving various geometric problems and proofs, as it provides essential information about the relationships between lines and angles.

Other Angles:

In addition to alternate angles, several other angle relationships occur when a transversal crosses parallel lines.

Detailed explanation

Practice Alternate angles

Test your knowledge with 48 quizzes

Which type of angles are shown in the figure below?

Examples with solutions for Alternate angles

Step-by-step solutions included
Exercise #1

Does the diagram show an adjacent angle?

Step-by-Step Solution

To solve this problem, we'll follow these steps:

  • Step 1: Inspect the given diagram for angles.
  • Step 2: Determine if any angles share a common vertex and a common side.
  • Step 3: Verify that the angles do not overlap.

Now, let's work through each step:

Step 1: Inspecting the diagram, we notice several intersecting lines.

Step 2: To check for adjacent angles, we look for pairs of angles that share both a common vertex and a common side. An adjacent angle must be formed by such pairs, ensuring they do not overlap.

Step 3: Based on our definition, after closely examining the diagram, no pair of angles in the diagram seems to satisfy the definition of adjacent angles. The intersecting lines form angles that don't share a common arm with any other angle at the same vertex in the manner required for adjacency.

Therefore, the solution to the problem is No, the diagram does not show an adjacent angle.

Answer:

No

Video Solution
Exercise #2

Is it possible to have two adjacent angles, one of which is obtuse and the other right?

Step-by-Step Solution

Remember the definition of adjacent angles:

Adjacent angles always complement each other up to one hundred eighty degrees, that is, their sum is 180 degrees.

This situation is impossible since a right angle equals 90 degrees, an obtuse angle is greater than 90 degrees.

Therefore, together their sum will be greater than 180 degrees.

Answer:

No

Video Solution
Exercise #3

Does the diagram show an adjacent angle?

Step-by-Step Solution

To determine whether the diagram shows adjacent angles, we need to confirm the presence of two properties:
1. Two angles must share a common vertex.
2. These angles must have a common arm and should not overlap.

Based on the given representation, the provided diagram consists solely of a single line. There are no visible intersecting lines or vertices from which angles can originate. Without intersection, there cannot be distinct angles, and thereby no adjacent angles can be identified.

Therefore, the diagram lacks the necessary properties to demonstrate adjacent angles. Hence, the correct choice is No.

Answer:

No

Video Solution
Exercise #4

Does the drawing show an adjacent angle?

Step-by-Step Solution

Adjacent angles are angles whose sum together is 180 degrees.

In the attached drawing, it is evident that there is no angle of 180 degrees, and no pair of angles can create such a situation.

Therefore, in the drawing there are no adjacent angles.

Answer:

Not true

Video Solution
Exercise #5

Does the drawing show an adjacent angle?

Step-by-Step Solution

Adjacent angles are angles whose sum together is 180 degrees.

In the attached drawing, it is evident that there is no angle of 180 degrees, and no pair of angles can create such a situation.

Therefore, in the drawing there are no adjacent angles.

Answer:

Not true

Video Solution

Frequently Asked Questions

Everything you need to know about Alternate angles

What are the different types of angles formed when parallel lines are cut by a transversal?

+
When parallel lines are cut by a transversal, eight angles are formed creating four main relationships: corresponding angles (equal), alternate interior angles (equal), alternate exterior angles (equal), and co-interior angles (supplementary - add to 180°). These relationships are fundamental to solving parallel line problems.

How do you find missing angles in parallel lines step by step?

+
To find missing angles in parallel lines: 1) Identify the parallel lines and transversal, 2) Determine which angle relationship applies (corresponding, alternate, or co-interior), 3) Set up an equation using the angle relationship, 4) Solve for the unknown angle, 5) Check your answer makes sense within the context.

What's the difference between corresponding angles and alternate angles?

+
Corresponding angles are in the same relative position at each intersection point and are always equal. Alternate angles are on opposite sides of the transversal - alternate interior angles are between the parallel lines, while alternate exterior angles are outside them, and both types are equal when lines are parallel.

Why do co-interior angles add up to 180 degrees?

+
Co-interior angles (also called consecutive interior angles) are supplementary because they form a straight line when extended. Since parallel lines maintain consistent angle relationships, these interior angles on the same side of the transversal must sum to 180° to preserve the parallel property.

What are the most common mistakes students make with parallel line angles?

+
Common mistakes include: • Confusing corresponding and alternate angles • Forgetting that co-interior angles are supplementary, not equal • Misidentifying which lines are parallel in complex diagrams • Not using vertically opposite angles when needed • Assuming all angles are equal without checking the relationship type

How are parallel line angles used in real life?

+
Parallel line angles appear in architecture (roof trusses, window frames), engineering (bridge construction, railway tracks), art and design (perspective drawing, tile patterns), and navigation (understanding map grids and compass bearings). These concepts help ensure structural stability and visual accuracy.

What grade level covers angles in parallel lines?

+
Angles in parallel lines are typically introduced in grades 7-8 as part of basic geometry, with more advanced applications in grades 9-10. The topic builds on prior knowledge of angle types and prepares students for proof-based geometry and trigonometry.

How do you prove that two lines are parallel using angles?

+
Lines can be proven parallel if: corresponding angles are equal, alternate interior angles are equal, alternate exterior angles are equal, or co-interior angles are supplementary (sum to 180°). If any of these conditions are met when lines are cut by a transversal, the lines must be parallel.

More Alternate angles Questions

Click on any question to see the complete solution with step-by-step explanations

Angles in Parallel Lines

Adjacent Angle Identification: Analyzing Line Intersection Diagram Adjacent Angles: Analyzing Intersecting Lines in Geometric Diagram Adjacent Angle Identification: Analyzing Geometric Line Intersections Geometry Problem: Identifying Adjacent Angle Relationships Adjacent Angles: Identifying Geometric Properties in Line Intersections

Continue Your Math Journey

Master Alternate angles first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

Parallel lines

Topics Learned in Later Sections

Angles In Parallel LinesCorresponding anglesCollateral anglesVertically Opposite AnglesAdjacent anglesCorresponding exterior anglesAlternate interior anglesPerpendicular Lines

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Using additional geometric shapes Isosceles triangle Three parallel lines Using angles in a triangle Using variables Generate a random angle Identifying and defining elements