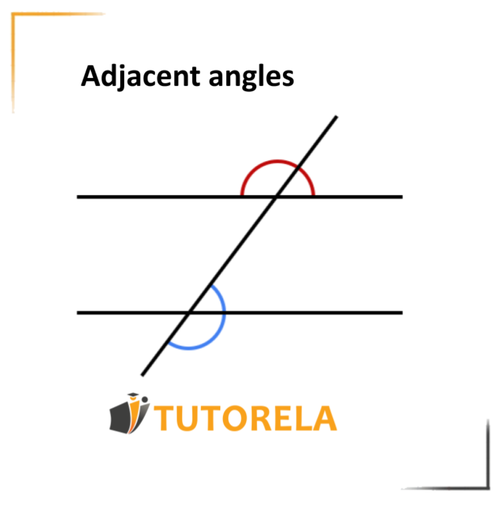
Adjacent Angles Practice Problems and Worksheets | Step-by-Step

Master adjacent angles with guided practice problems. Learn to identify, calculate, and solve adjacent angle relationships in parallel lines and intersecting lines.

📚What You'll Master in Adjacent Angles Practice
  • Identify adjacent angles formed when two straight lines intersect
  • Apply the supplementary property: adjacent angles always sum to 180°
  • Distinguish between adjacent, corresponding, alternate, and opposite angles
  • Solve for unknown angles using adjacent angle relationships
  • Work with adjacent angles in parallel lines and transversal problems
  • Calculate missing angles in triangles using adjacent angle properties

Understanding Adjacent angles

Complete explanation with examples

What does adjacent angle mean?

Adjacent angles are the pair of angles formed when two lines intersect each other. These angles are formed at the point where the intersection occurs, and are adjacent to eachother - hence its name. Another pair of angles that are formed at the intersection of two straight lines are the opposite angles, but this pair of angles are opposite at the vertex and not adjacent, so we should not confuse them with adjacent angles. Adjacent angles are always supplementary, that is, together they equal 180° 180° .

The following illustration shows two examples of what adjacent angles look like. One example is red and the other blue.

Adjacent angles new

Detailed explanation

Practice Adjacent angles

Test your knowledge with 48 quizzes

Does the diagram show an adjacent angle?

Examples with solutions for Adjacent angles

Step-by-step solutions included
Exercise #1

Identify the angle shown in the figure below?

Step-by-Step Solution

Remember that adjacent angles are angles that are formed when two lines intersect one another.

These angles are created at the point of intersection, one adjacent to the other, and that's where their name comes from.

Adjacent angles always complement one another to one hundred and eighty degrees, meaning their sum is 180 degrees. 

Answer:

Adjacent

Exercise #2

Identify the angles shown in the diagram below?

Step-by-Step Solution

Let's remember that vertical angles are angles that are formed when two lines intersect. They are are created at the point of intersection and are opposite each other.

Answer:

Vertical

Exercise #3

Which type of angles are shown in the figure below?

Step-by-Step Solution

Alternate angles are a pair of angles that can be found on the opposite side of a line that cuts two parallel lines.

Furthermore, these angles are located on the opposite level of the corresponding line that they belong to.

Answer:

Alternate

Exercise #4

Which type of angles are shown in the diagram?

Step-by-Step Solution

First let's remember that corresponding angles can be defined as a pair of angles that can be found on the same side of a transversal line that intersects two parallel lines.

Additionally, these angles are positioned at the same level relative to the parallel line to which they belong.

Answer:

Corresponding

Exercise #5

a a is parallel to

b b

Determine which of the statements is correct.

αααβββγγγδδδaaabbb

Step-by-Step Solution

Let's review the definition of adjacent angles:

Adjacent angles are angles formed where there are two straight lines that intersect. These angles are formed at the point where the intersection occurs, one next to the other, and hence their name.

Now let's review the definition of collateral angles:

Two angles formed when two or more parallel lines are intersected by a third line. The collateral angles are on the same side of the intersecting line and even are at different heights in relation to the parallel line to which they are adjacent.

Therefore, answer C is correct for this definition.

Answer:

β,γ \beta,\gamma Colateralesγ,δ \gamma,\delta Adjacent

Video Solution

Frequently Asked Questions

Everything you need to know about Adjacent angles

What are adjacent angles and how do I identify them?

+
Adjacent angles are pairs of angles formed when two straight lines intersect at a point. They share a common vertex and are next to each other (adjacent). The key property is that adjacent angles are always supplementary, meaning they add up to exactly 180°.

How do I solve adjacent angle problems step by step?

+
Follow these steps: 1) Identify the adjacent angle pair at the intersection point, 2) Set up the equation knowing they sum to 180°, 3) Substitute known angle measures, 4) Solve for the unknown angle by subtracting the known angle from 180°.

What's the difference between adjacent angles and corresponding angles?

+
Adjacent angles form at the same intersection point and are supplementary (sum to 180°). Corresponding angles occur when parallel lines are cut by a transversal, are in matching positions, and are equal to each other, not supplementary.

Can two obtuse angles be adjacent to each other?

+
No, two obtuse angles cannot be adjacent. Since obtuse angles are greater than 90°, two of them would sum to more than 180°. Adjacent angles must be supplementary (sum to exactly 180°), so at least one must be acute.

How do adjacent angles help solve triangle problems?

+
Adjacent angles are useful when triangle sides are extended to show exterior angles. The exterior angle and its corresponding interior angle are adjacent and supplementary. This relationship helps find missing interior angles when combined with the triangle angle sum property (180°).

What are the most common mistakes with adjacent angles?

+
Common errors include: confusing adjacent with opposite angles (which are equal, not supplementary), forgetting that adjacent angles must sum to 180°, and misidentifying angle pairs in parallel line diagrams. Always check that angles share a vertex and are next to each other.

How do I work with adjacent angles in parallel line problems?

+
In parallel line problems, first identify if you're dealing with adjacent angles (at intersection points) or other angle relationships like corresponding or alternate angles. Adjacent angles will always be supplementary regardless of whether the lines are parallel.

What formulas do I need for adjacent angle calculations?

+
The main formula is: Adjacent Angle 1 + Adjacent Angle 2 = 180°. If one angle measures x°, then its adjacent angle measures (180 - x)°. This supplementary relationship is the foundation for all adjacent angle problems.

More Adjacent angles Questions

Click on any question to see the complete solution with step-by-step explanations

Angles in Parallel Lines

Calculate α + B: Geometric Angle Addition with Parallel Lines Co-interior Angles: Identifying α, β, γ, δ Between Parallel Lines Find Angle α in Geometric Diagram with 120° Reference Co-interior Angles: Identifying α1, β1, α2, β2 with Parallel Lines Calculate 7 Angles with Parallel Lines: Given Angle 115°

Continue Your Math Journey

Master Adjacent angles first, then advance to these related topics that build on your fraction skills

Suggested Topics to Practice in Advance

Parallel lines

Topics Learned in Later Sections

Angles In Parallel LinesAlternate anglesCorresponding anglesCollateral anglesVertically Opposite AnglesCorresponding exterior anglesAlternate interior anglesPerpendicular Lines

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Generate a random angle Identifying and defining elements Isosceles triangle Three parallel lines Using additional geometric shapes Using angles in a triangle Using variables