So far we have worked with common two-dimensional figures such as the square or the triangle.
Three-dimensional figures are those that extend into the third dimension, meaning that in addition to length and width, they also have height (that is, the figure has depth).
Cuboids Practice Problems & Three-Dimensional Figures
Master cuboids, cylinders, and prisms with step-by-step practice problems. Calculate volume, surface area, and lateral area of 3D shapes with detailed solutions.
📚Practice Three-Dimensional Figures and Build Your Geometry Skills
- Calculate volume of cuboids using length × width × height formula
- Find surface area of rectangular prisms with complete step-by-step solutions
- Determine lateral area of cuboids excluding the top and bottom faces
- Solve cylinder volume problems using πr²h formula with real measurements
- Calculate total surface area of cylinders including bases and lateral surface
- Work with triangular prism volume and area calculations
Understanding Cuboids
Complete explanation with examples
Three-dimensional figures
What are three-dimensional figures?
What differences do three-dimensional figures have?
Three-dimensional figures have several definitions that we will see next:
Below is a three-dimensional figure that we will use to learn each definition - The cube:
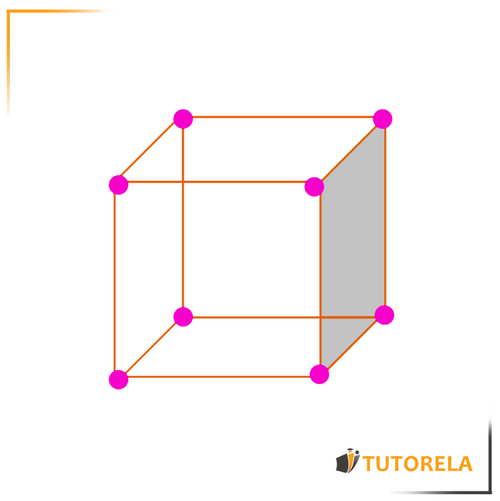
Face: it is the flat side of a three-dimensional figure
In the cube we have here, there are 6 faces (one of them is painted gray)
Edge: these are the lines that connect one face to another in a three-dimensional figure
In the cube we have here, there are 12 edges (painted green)
Vertex: it is the point that connects the edges
In the cube we have here, there are 8 vertices (painted orange)
Volume: it is the amount of space contained within a three-dimensional figure.
The units of measurement are .
Practice Cuboids
Test your knowledge with 25 quizzes
An orthohedron has the dimensions: 4, 7, 10.
How many rectangles is it formed of and what are their dimensions?
Examples with solutions for Cuboids
Step-by-step solutions included
Exercise #1
A cuboid has the dimensions shown in the diagram below.
Which rectangles form the cuboid?
Step-by-Step Solution
Every cuboid is made up of rectangles. These rectangles are the faces of the cuboid.
As we know that in a rectangle the parallel faces are equal to each other, we can conclude that for each face found there will be two rectangles.
Let's first look at the face painted orange,
It has width and height, 5 and 3, so we already know that they are two rectangles of size 5x6
Now let's look at the side faces, they also have a height of 3, but their width is 6,
And then we understand that there are two more rectangles of 3x6
Now let's look at the top and bottom faces, we see that their dimensions are 5 and 6,
Therefore, there are two more rectangles that are size 5x6
That is, there are
2 rectangles 5X6
2 rectangles 3X5
2 rectangles 6X3
Answer:
Two 5X6 rectangles
Two 3X5 rectangles
Two 6X3 rectangles
Video Solution
Exercise #2
Look at the the cuboid below.
What is its surface area?
Step-by-Step Solution
First, we recall the formula for the surface area of a cuboid:
(width*length + height*width + height*length) *2
As in the cuboid the opposite faces are equal to each other, the given data is sufficient to arrive at a solution.
We replace the data in the formula:
(8*5+3*5+8*3) *2 =
(40+15+24) *2 =
79*2 =
158
Answer:
158
Video Solution
Exercise #3
Identify the correct 2D pattern of the given cuboid:
Step-by-Step Solution
Let's go through the options:
A - In this option, we can observe that there are two flaps on the same side.
If we try to turn this net into a box, we should obtain a box where on one side there are two faces one on top of the other while the other side is "open",
meaning this net cannot be turned into a complete and full box.
B - This net looks valid at first glance, but we need to verify that it matches the box we want to draw.
In the original box, we see that we have four flaps of size 9*4, and only two flaps of size 4*4,
if we look at the net we can see that the situation is reversed, there are four flaps of size 4*4 and two flaps of size 9*4,
therefore we can conclude that this net is not suitable.
C - This net at first glance looks valid, it has flaps on both sides so it will close into a box.
Additionally, it matches our drawing - it has four flaps of size 9*4 and two flaps of size 4*4.
Therefore, we can conclude that this net is indeed the correct net.
D - In this net we can see that there are two flaps on the same side, therefore this net will not succeed in becoming a box if we try to create it.
Answer:
Exercise #4
Look at the cuboid below.
What is the surface area of the cuboid?
Step-by-Step Solution
Let's see what rectangles we have:
8*5
8*12
5*12
Let's review the formula for the surface area of a rectangular prism:
(length X width + length X height + width X height) * 2
Now let's substitute all this into the exercise:
(8*5+12*8+12*5)*2=
(40+96+60)*2=
196*2= 392
This is the solution!
Answer:
392 cm²
Video Solution
Exercise #5
A cuboid is shown below:
What is the surface area of the cuboid?
Step-by-Step Solution
Remember that the formula for the surface area of a cuboid is:
(length X width + length X height + width X height) 2
We input the known data into the formula:
2*(3*2+2*5+3*5)
2*(6+10+15)
2*31 = 62
Answer:
62
Video Solution
Frequently Asked Questions
How do you calculate the volume of a cuboid step by step?
+To find the volume of a cuboid, multiply length × width × height. For example, if a cuboid has dimensions 5 cm × 3 cm × 4 cm, the volume is 5 × 3 × 4 = 60 cm³. Always include cubic units in your final answer.
What is the difference between surface area and lateral area of a cuboid?
+Surface area includes all 6 faces of the cuboid using the formula 2(lw + hw + hl). Lateral area only includes the 4 side rectangles, excluding the top and bottom, calculated as 2h(l + w).
How many faces, edges, and vertices does a cuboid have?
+A cuboid has:
• 6 faces (rectangles that form the surface)
• 12 edges (lines where faces meet)
• 8 vertices (corner points where edges connect)
What is the formula for cylinder volume and when do you use it?
+The cylinder volume formula is V = πr²h, where r is the radius of the circular base and h is the height. Use this when you need to find how much space is inside a cylindrical container or object.
How do you find the total surface area of a cylinder?
+Use the formula: Total Surface Area = 2πrh + 2πr². This includes the lateral (curved) surface area (2πrh) plus the area of both circular bases (2πr²). Remember to use π ≈ 3.14 in calculations.
What makes a triangular prism different from other 3D shapes?
+A triangular prism has 2 identical triangular bases connected by 3 rectangular faces. Unlike cuboids with all rectangular faces, or cylinders with circular bases, triangular prisms combine triangular and rectangular surfaces.
When solving 3D geometry problems, what measurements do I need?
+For cuboids: length, width, height
For cylinders: radius (or diameter) and height
For triangular prisms: base triangle measurements and prism height
Always check which specific calculation (volume, surface area, or lateral area) is required.
How do face diagonals differ from space diagonals in a cuboid?
+Face diagonals connect two vertices on the same rectangular face of the cuboid. Space diagonals (also called body diagonals) connect vertices from opposite corners of the entire cuboid, passing through the interior space.