Angles Practice Problems: Sides, Vertices & Geometry

Master angles, sides, and vertices with step-by-step practice problems. Learn triangle angles, parallel lines, and polygon properties through guided exercises.

📚What You'll Master in This Angles Practice Session
  • Calculate unknown angles using triangle angle sum properties (180°)
  • Find angles between parallel lines using supplementary relationships
  • Identify and count sides, vertices, and angles in polygons
  • Solve problems involving adjacent angles and linear pairs
  • Apply angle properties to find missing measurements in geometric figures
  • Work with acute, right, obtuse, and straight angles in real contexts

Understanding Angles

Complete explanation with examples

Triangle

Understanding Sides, Vertices, and Angles in Geometry

In geometry, shapes are defined by three key components: sides, vertices, and angles. These elements work together to form polygons and other figures, helping us understand their properties and relationships.

The number of sides in a polygon equals the number of vertices and angles. For example, a hexagon has six sides, six vertices, and six angles.

Definitions:

Side

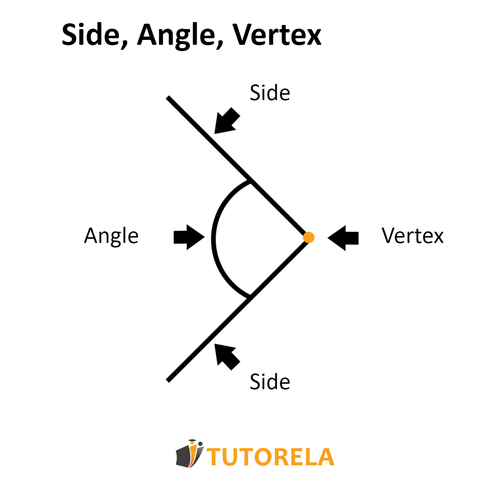
A side is the straight line that lies between two points called vertices. An angle is formed between two lines. Sides form the edges of a polygon. For example, a triangle has three sides, while a square has four. The length and arrangement of sides determine the size and shape of a figure.

Vertex

A vertex is the point of origin where two or more straight lines meet, thus creating an angle. These vertices are often referred to as the "corners" of a shape. A triangle has three vertices, a square has four, and a pentagon has five.

Angle

An angle is created when two lines originate from the same vertex.  The measure of an angle indicates the degree of rotation between the two sides. Angles can be acute (less than 90∘90^\circ), right (90∘90^\circ), obtuse (greater than 90∘90^\circ), or straight (180∘180^\circ).

To clearly illustrate these concepts, we will represent them in the following drawing:

A1 - Side, Angle, Vertex

Detailed explanation

Practice Angles

Test your knowledge with 52 quizzes

Find the measure of the angle \( \alpha \)

808080AAABBBCCC55

Examples with solutions for Angles

Step-by-step solutions included
Exercise #1

Identify the angle shown in the figure below?

Step-by-Step Solution

Remember that adjacent angles are angles that are formed when two lines intersect one another.

These angles are created at the point of intersection, one adjacent to the other, and that's where their name comes from.

Adjacent angles always complement one another to one hundred and eighty degrees, meaning their sum is 180 degrees. 

Answer:

Adjacent

Exercise #2

Indicates which angle is greater

Step-by-Step Solution

Note that in drawing B, the two lines form a right angle, which is an angle of 90 degrees:

While the angle in drawing A is greater than 90 degrees:

Therefore, the angle in drawing A is larger.

Answer:

Video Solution
Exercise #3

Indicates which angle is greater

Step-by-Step Solution

In drawing A, we can see that the angle is an obtuse angle, meaning it is larger than 90 degrees:

While in drawing B, the angle is a right angle, meaning it equals 90 degrees:

Therefore, the larger angle appears in drawing A.

Answer:

Video Solution
Exercise #4

Which angle is greater?

Step-by-Step Solution

The angle in diagram (a) is more acute, meaning it is smaller:

Conversely, the angle in diagram (b) is more obtuse, making it larger.

Answer:

Video Solution
Exercise #5

Indicates which angle is greater

Step-by-Step Solution

Answer B is correct because the more closed the angle is, the more acute it is (less than 90 degrees), meaning it's smaller.

The more open the angle is, the more obtuse it is (greater than 90 degrees), meaning it's larger.

Answer:

Video Solution

Frequently Asked Questions

Everything you need to know about Angles

How do you find missing angles in triangles?

+
Use the triangle angle sum theorem: all angles in a triangle add up to 180°. If you know two angles, subtract their sum from 180° to find the third angle. For example, if two angles are 53° and 86°, the third angle is 180° - 53° - 86° = 41°.

What is the relationship between sides, vertices, and angles in polygons?

+
In any polygon, the number of sides equals the number of vertices and angles. A triangle has 3 sides, 3 vertices, and 3 angles. A square has 4 of each. This relationship helps identify and classify different geometric shapes.

How do you calculate angles with parallel lines?

+
When parallel lines are cut by a transversal, several angle relationships form: 1) Corresponding angles are equal, 2) Alternate interior angles are equal, 3) Same-side interior angles are supplementary (add to 180°). Use these properties to find unknown angles.

What are the different types of angles and their measures?

+
Angles are classified by their measures: Acute angles are less than 90°, right angles equal exactly 90°, obtuse angles are greater than 90° but less than 180°, and straight angles equal 180°. These classifications help solve geometry problems.

How do you identify vertices in geometric shapes?

+
A vertex is where two or more lines meet, forming a corner. To identify vertices: 1) Look for intersection points of sides, 2) Count the corners of the shape, 3) Remember that each vertex creates an angle. Triangles have 3 vertices, squares have 4.

What is the difference between adjacent and opposite angles?

+
Adjacent angles share a common vertex and side but don't overlap. They often form linear pairs that add to 180°. Opposite angles (vertical angles) are across from each other when two lines intersect and are always equal in measure.

How do you solve angle problems step by step?

+
Follow these steps: 1) Identify what type of angle relationship exists, 2) Write an equation using angle properties (sum = 180° for triangles), 3) Substitute known values, 4) Solve for the unknown angle, 5) Check your answer makes geometric sense.

Why do triangle angles always sum to 180 degrees?

+
This is a fundamental geometric theorem. When you draw any triangle and extend one side, the exterior angle equals the sum of the two non-adjacent interior angles. This relationship proves that all three interior angles must total 180°, making it a reliable problem-solving tool.

More Angles Questions

Click on any question to see the complete solution with step-by-step explanations

Sum and Difference of Angles

Triangle Angle Analysis: Can 30°, 60°, and 90° Form a Valid Triangle? Triangle Angle Verification: Do 56°, 89°, and 17° Form a Valid Triangle? Calculate Angle X in Straight Line: Given 41° and 45° Angles Find the Missing Angle: Geometric Construction with 36° Arc Segment Find the Missing Angle in an 80° Angle Problem

Angles

Parallel Line Geometry: Classifying Triangle ABC with Extended Side AE Find Triangle Angles: Isosceles Triangle with 76° and Parallel Lines Parallel Lines and Angle Properties: Analyzing α, β, γ, and δ Relationships Parallel Lines a and b: Analyzing Adjacent Angle Properties Co-interior Angles in Parallel Lines: Identifying α, β, γ, and δ

Practice by Question Type

Choose your preferred learning style and practice format for fraction problems
Angle bisector Applying the formula Calculate Angles in Quadrilaterals Finding the size of angles in a triangle Generate a random angle Identifying and defining elements Identify the greater value Is it possible...? Isosceles triangle Using angles in a triangle Using quadrilaterals Using ratios for calculation Using variables

More Resources and Links

Explore more resources and links related to Angles
Practice Angle NotationPractice Angle BisectorPractice Types of AnglesPractice Right anglePractice Acute AnglesPractice Obtuse AnglePractice Plane anglePractice Sum and Difference of AnglesPractice Sum of Angles in a PolygonPractice The Sum of the Interior Angles of a TrianglePractice Exterior angles of a trianglePractice Types of angles (right, acute, obtuse, straight)