Converting a simple fraction to decimal - how to calculate?

Converting Decimal Fractions to Simple Fractions and Mixed Numbers - Examples, Exercises and Solutions
🏆Practice converting decimal fractions to simple fractions and mixed numbers
5 Questions
Decimal Fractions - Basic
Converting Decimal Fractions to Simple Fractions and Mixed Numbers
Practice
Add a new subject

Converting a simple fraction to decimal - how to calculate?

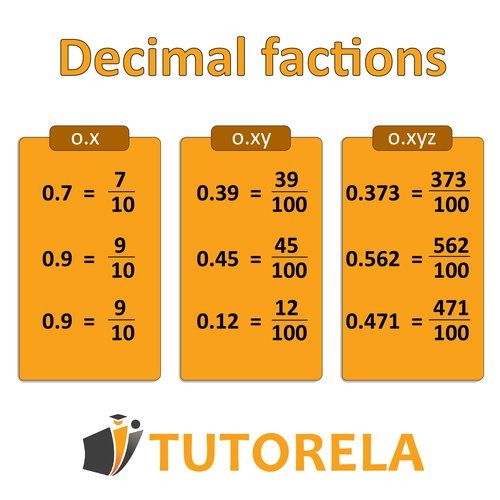
So how do we convert a simple fraction to a decimal fraction? First, we can reassure you by saying that the answer is: quite easily. All you need is to understand the technique, and mainly to understand the meaning of the decimal fraction. First, what do decimal fractions look like? They appear in the following form: 0.5, 3.6, and so on. Or in other words: "the fraction with the point".

In fact, there is a point that creates the boundary between the whole number and the fraction. To convert a simple fraction to a decimal fraction, you need to choose a denominator: 10, 100, or 1000. So how can you also convert "simple" fractions to decimal fractions? Pay attention:

Basic fraction data:

  • The line that separates between two different numbers is called the fraction line.
  • The top part of the fraction - numerator.
  • The bottom part of the fraction - denominator.

Note that when we convert a "classic" simple fraction to a decimal fraction, the fraction line disappears, and a decimal point separates the numbers.

Chart illustrating the conversion of decimal numbers to fractions, categorized by one-digit, two-digit, and three-digit decimals, including examples like 0.7 = 7/10 and 0.562 = 562/100.

Start practice

Test yourself on converting decimal fractions to simple fractions and mixed numbers!

How much of the whole does the shaded area (blue) represent?

Practice more now

Converting a simple fraction to decimal - how to calculate?

So how do we convert a simple fraction to a decimal fraction? First, we can reassure you by saying that the answer is: quite easily. All you need is to understand the technique, and mainly to understand the meaning of the decimal fraction. First, how do decimal fractions look? They appear in the following form: 0.5, 3.6, and so on. Or in other words: "the fraction with the point".

Actually, there is a point that creates the boundary between the whole number and the fraction. To convert a simple fraction to a decimal fraction, you need to choose a denominator: 10, 100, or 1000. So how can you also convert "simple" fractions to decimal fractions? Pay attention:

Basic fraction data:

  • The line that separates between the two different numbers is called the fraction bar.
  • The top part of the fraction - numerator.
  • The bottom part of the fraction - denominator.

Note that when we convert a "classic" simple fraction to a decimal fraction, the fraction line disappears, and a decimal point separates the numbers.

Calculation method: How do we convert a simple fraction to a decimal?

Let's say we have the fraction 252\over5. In order to reach the denominator 1010 (remember, we need to choose a denominator), we'll need to multiply both the numerator and the denominator by 22. Thus, the fraction changes from 252\over5 to 4104\over10. Therefore, our decimal number will be 0.40.4.

Another example:

Given the fraction 121\over2. First, we need to obtain a denominator of 1010, which means we'll need to multiply both the numerator and the denominator by 55. Thus, the resulting fraction will be 5105\over10, and the decimal fraction will be 0.50.5.

Additional Examples - Converting a Simple Fraction to Decimal

Given the fraction 151\over5. The chosen denominator in this case will be 1010, thus we need to multiply both the numerator and the denominator by 22.
Now, the fraction changes to 2102\over10, so in its decimal form it will be 0.20.2.

Given the fraction 1251\over25. The chosen denominator in this case will be 100100. Now, we'll multiply both the numerator and the denominator by 44.
The fraction changes to 41004 \over 100, which means in its decimal form it will be 0.040.04.

Given the fraction 22502\over250. The chosen denominator in this case will be 10001000. Now, we'll multiply both the numerator and the denominator by 44.
The fraction will be 810008\over1000, and in its decimal form it will be 0.0080.008.

Join Over 30,000 Students Excelling in Math!
Endless Practice, Expert Guidance - Elevate Your Math Skills Today
Test your knowledge
Question 1

How much of the whole does the shaded area (blue) represent?

Question 2

How much of the whole does the shaded area (blue) represent?

Question 3

How much of the whole does the shaded area (blue) represent?

Examples with solutions for Converting Decimal Fractions to Simple Fractions and Mixed Numbers

Exercise #1

How much of the whole does the shaded area (blue) represent?

Step-by-Step Solution

To solve this problem, we will determine how much of the whole grid is represented by the shaded area.

The problem provides a 10x10 grid which contains 100 smaller squares in total. Our task is to determine how many of these squares are shaded.

Upon inspection, we count that 80 out of the 100 squares are shaded.

Therefore, the fraction of the whole that the shaded area represents is given by dividing the number of shaded squares by the total number of squares:

shaded squarestotal squares=810 \frac{\text{shaded squares}}{\text{total squares}} = \frac{8}{10}

Converting this fraction to a decimal gives 0.80.8.

Thus, the shaded area represents 810\frac{8}{10} or 0.80.8 of the whole.

Among the choices provided, the correct answer is: 0.8 0.8 or 810 \frac{8}{10} .

Answer

0.8 0.8 or 810 \frac{8}{10}

Exercise #2

How much of the whole does the shaded area (blue) represent?

Step-by-Step Solution

To solve this problem, we need to determine the fraction of the whole grid that is represented by the shaded (blue) area. The grid is a 10x10 layout, therefore containing a total of 10×10=10010 \times 10 = 100 equal-sized squares.

Step 1: We count the number of shaded squares in the grid. According to the illustration, there are 86 shaded squares.

Step 2: Calculate the fraction of the shaded area compared to the whole grid: Number of shaded squaresTotal number of squares=86100\frac{\text{Number of shaded squares}}{\text{Total number of squares}} = \frac{86}{100}.

Step 3: Convert this fraction into a decimal. Dividing the numerator by the denominator gives us 0.86 0.86 .

Therefore, the shaded area represents 86100\frac{86}{100} of the total grid, which is equivalent to 0.860.86.

This matches with the correct answer choice, which is: 0.860.86 or 86100\frac{86}{100}.

Answer

0.86 0.86 or 86100 \frac{86}{100}

Exercise #3

Convert into fraction form:

0.04= 0.04=

Video Solution

Step-by-Step Solution

Let's pay attention to where the decimal point is located in the number.

Remember:

One number after the zero represents tens

Two numbers after the zero represent hundreds

Three numbers after the zero represent thousands

And so on

In this case, there are two numbers after the zero, so the number is divided by 100

Let's write the fraction in the following way:

004100 \frac{004}{100}

We'll then remove the unnecessary zeros as follows:

4100 \frac{4}{100}

Answer

4100 \frac{4}{100}

Exercise #4

Convert into fraction form:

0.06= 0.06=

Video Solution

Step-by-Step Solution

Let's pay attention to where the decimal point is located in the number.

Remember:

One number after the zero represents tens

Two numbers after the zero represent hundreds

Three numbers after the zero represent thousands

And so on

In this case, there are two numbers after the zero, so the number is divided by 100

We'll write the fraction like this:

006100 \frac{006}{100}

We'll then remove the unnecessary zeros as follows:

6100 \frac{6}{100}

Answer

6100 \frac{6}{100}

Exercise #5

Convert into fraction form:

0.33= 0.33=

Video Solution

Step-by-Step Solution

Let's pay attention to where the decimal point is located in the number.

Remember:

One number after the zero represents tens

Two numbers after the zero represent hundreds

Three numbers after the zero represent thousands

And so on

In this case, there are two numbers after the zero, so the number is divided by 100

We'll write the fraction in the following way:

033100 \frac{033}{100}

We'll then proceed to remove the unnecessary zeros as follows:

33100 \frac{33}{100}

Answer

33100 \frac{33}{100}

Start practice

More Questions

👉  Click here  to practice