Parts of a Rectangular Prism

The rectangular prism is a three-dimensional figure composed of $6$ rectangles.

Every rectangular prism has:
$6$ faces -> rectangles that make up the rectangular prism.
$12$ edges -> (in length, width, and height).
$8$ vertices -> the corners where the edges meet.

Detailed explanation

Start practice

Test yourself on parts of a cuboid!

How many diagonals identical to the dotted diagonal in the diagram are there in the rectangular prism?

Practice more now

The parts of a rectangular prism

Rectangular prism! What a magnificent figure!
In this article, we will learn about the rectangular prism and its parts.

What is a rectangular prism?

A rectangular prism can look like this:

like this:

even like this:

As long as it is a three-dimensional figure composed of $6$ rectangles, it will be a rectangular prism.
In the case that all the rectangles are equivalent, that is, length = width = height, we would be talking about a cube.

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

How many edges does a cuboid have?

Question 2

Look at the cuboid in the figure.

Which of the following is an edge of the given cuboid?

Question 3

Look at the dotted diagonal in the figure below.

Which diagonals of the rectangular prism are equal?

Parts of a Rectangular Prism

Now let's see what parts make up a rectangular prism

Faces

The rectangles that make up the rectangular prism are called faces,
therefore, the rectangular prism has $6$ faces:

Do you know what the answer is?

Question 1

The number of faces in the cuboid is:

Question 2

The number of vertices in the cuboid is:

Question 3

The quadrilateral of the cuboid is:

Edges

The rectangular prism has $12$ edges or sides.
Let's see them painted orange in the illustration:

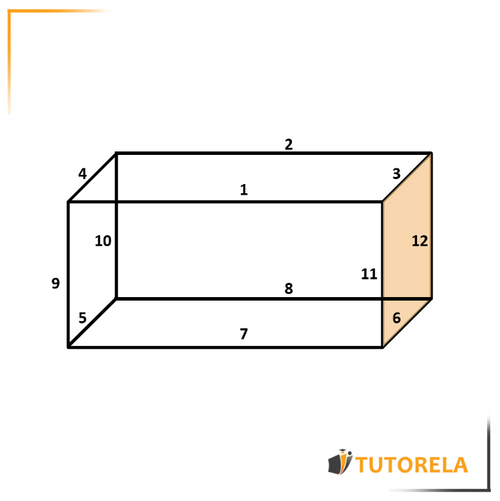
More data about the edges

The rectangular prism has length, width, and height.
The width edge is identical to all the other width edges of the rectangular prism, there are $4$ like it.
The length edge is identical to all the other length edges of the rectangular prism, there are $4$ like it.
The height edge is identical to all the other height edges of the rectangular prism, there are $4$ like it.
Let's see what it's about in the illustration:

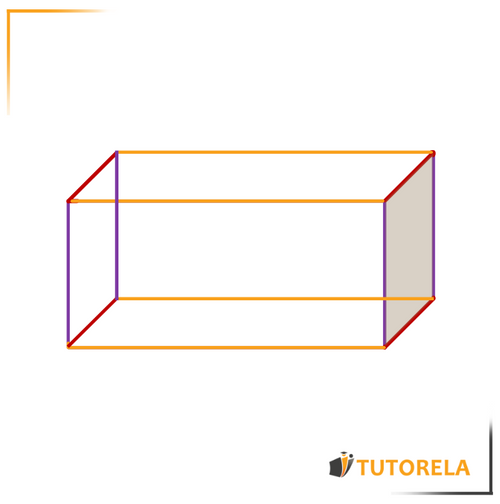
The orthohedron has length, width, and height

Height: marked in yellow
Width: marked in red
Height: marked in purple (violet)

Note: when it comes to a cube, the length is = to the width, which is also = to the height.

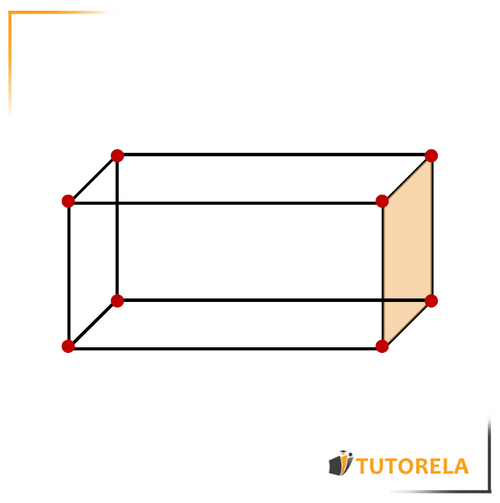
Vertices

The vertices are those that join the edges of the rectangular prism.
Each rectangular prism has $8$ vertices.
Let's see them painted red in the illustration:

Check your understanding

Question 1

The volume of the cuboid is es:

Question 2

Which is the longest line indicated in the diagram?

Question 3

Which of the line segments is the diagonal of the rectangular prism?

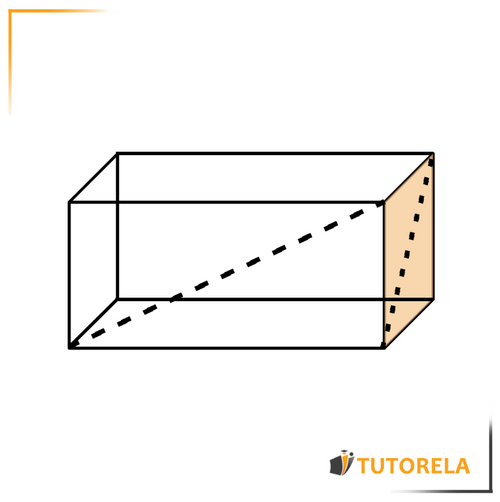
Face Diagonals

The diagonals that go from one vertex to another on the same face are called external diagonals.
The $2$ vertices must belong to the same face.
Let's see an example in the illustration:

Diagonals of the Rectangular Prism

The diagonals that go from one vertex to another vertex of a different face are called the diagonals of the orthohedron or internal diagonals.
The $2$ vertices are not on the same face.
Let's see an example in the illustration:

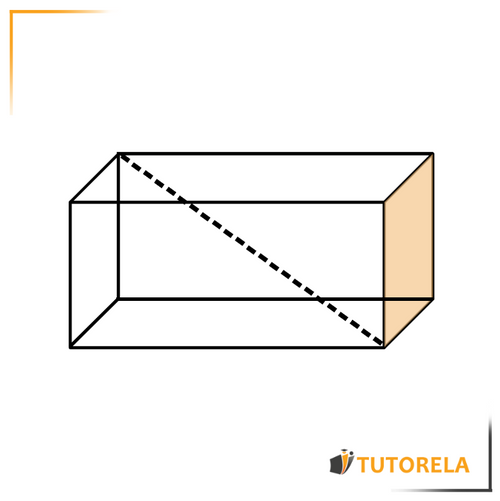
Exercise:
How many vertices are there in the rectangular prism?

Answer:
$8$ vertices.

How many faces are there in the rectangular prism?
Answer:
$6$ faces.

How many edges are there in the rectangular prism?

A.   $6$
B.   $12$
C.   $14$
D.   $8$

Answer: B. $12$ edges.

Examples and exercises with solutions of the parts of a rectangular prism

Exercise #1

How many edges does a cuboid have?

Video Solution

Step-by-Step Solution

"Edges" is the name of the box's sides. Since a box is a three-dimensional shape, we call these parts edges.

Counting the edges of a box, we can see that there arehas 12 edges:

Answer

$12$

Exercise #2

Look at the dotted diagonal in the figure below.

Which diagonals of the rectangular prism are equal?

Video Solution

Step-by-Step Solution

Let's look at the face AEHD

In it, there is another diagonal equal to ED, which is AH

Let's look at the face BFGC which is identical and equal to AEHD, in which there are two diagonals that are also equal to ED:

$FC=BG=ED$

Answer

$AH,BG,FC$

Exercise #3

Which of the line segments is the diagonal of the rectangular prism?

Video Solution

Step-by-Step Solution

A box diagonal is a diagonal that passes between two vertices that are not connected,
meaning, the diagonal passes through the box, and not on one of its edges.

Let's see which of the segments in the answers passes entirely through the box from end to end.

AC, HF and FC are all diagonals that lie on the edges of the box, therefore the segment that fits this description is BH.

Answer

$BH$

Exercise #4

How many diagonals identical to the dotted diagonal in the diagram are there in the rectangular prism?

Video Solution

Answer

$4$

Exercise #5

Look at the cuboid in the figure.

Which of the following is an edge of the given cuboid?

Video Solution

Answer

Do you think you will be able to solve it?

Question 1

Which of the shapes has a dotted diagonal equal in length to the dotted diagonal shown below?

Question 2

Choose the dimensions that represent an orthohedron with a square base.

Question 3

Choose the dimensions that represent an orthohedron with a square base.

Start practice