Regular Polygon

Regular tessellation is created by covering a surface with isometric (identical) copies of an initial figure and "attaching" them to the edge of another regular polygon.
This way, it happens that the sum of the angles at each vertex is $360$!
We can achieve $3$ tessellations of this type with triangles, squares, and hexagons.
Let's see it in an illustration:

Tessellation with triangles

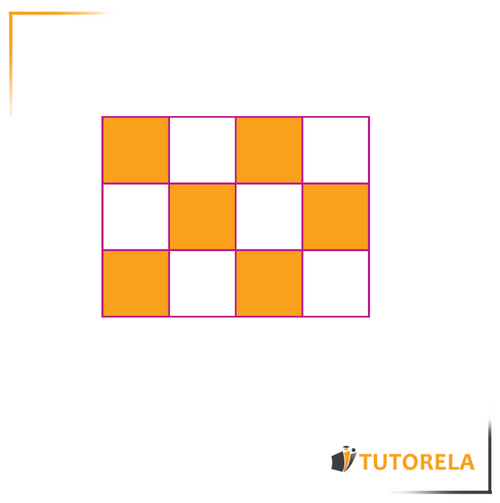
Tessellation with squares

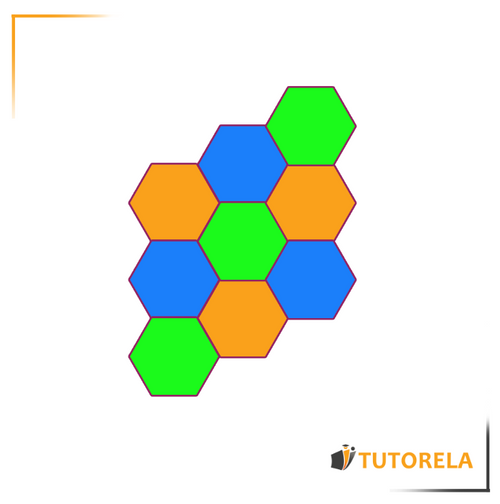
Tessellation with regular hexagons

In fact, the formula to find the sum of the angles of a regular polygon is the same as the formula to find the sum of the angles of any polygon, which is:

$180\times (n-2) =~sum~of~the~angles~of~a~polygon$

where, $n$ = number of edges of the polygon

By observing this formula, you have surely realized that the sum of the angles of a polygon depends on the number of edges the polygon has.

Let's practice:
Let's look at the following polygon.

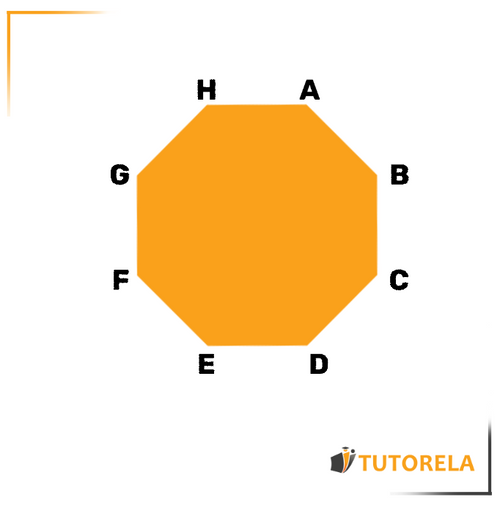
Find the size of angle $H$ and determine if it is a regular polygon knowing that:

• All sides are equal
• $∢A=∢B=∢C=∢D=∢E=∢F=∢G=135$
• Solution:
  To determine if the polygon is regular, we must show that all its sides and all its angles are equal.
  We know that all its sides are equal.
  To show that all its angles are equal, we will calculate the sum of the angles using the following formula:
  $180\times(8-2)=1080$
  $1080$ is the total of the angles of the polygon.
  We know that each of the $7$ angles measures $135$ so we will solve for the measure of the unknown angle:
  $1080-(7\times135)=$
  $1080-945=135$
  We have discovered that angle $H$ also equals $135$, therefore, the polygon is regular since all its sides and all its angles are equal.
• For more information on the sum of the angles of a polygon click here

To discover the measure of the angles in a regular polygon, all you have to do is apply the following formula:

$\frac{180\times(n-2)}{n}=~size~of~the~internal~angle~in~a~regular~polygon$

when, $n$ = number of edges of the polygon

We already know that in a regular polygon all the angles are equal.
Therefore, if you look at the formula, you will see that it takes the sum of the angles of the polygon and divides it by the number of angles it has, since, as we know, they all measure the same.

Let's practice:
Given a regular polygon with $7$ sides.
How much does each angle measure?

Solution:
We simply place in the formula $n=7$ and we get:

$\frac{180\times(7-2)}7=$

$\frac{180\times5}7=128.571$
Each angle of the regular polygon is equivalent to $128.571$

Another exercise:
Given a regular octagon:
Find the measure of its angle.

Solution:
We simply place in the formula $n=8$ and we get:

$\frac{180\times(8-2)}8=$

$\frac{180\times6}8=135$

Each angle of the regular octagon is equivalent to $135$

You can read again about the angles of a regular polygon by clicking here

To calculate the area of a regular hexagon, all you need to do is remember the following formula:

$6 \times \frac{a^2 \sqrt3}{4}$

where, $a$ = length of the side of the regular hexagon

Let's practice!
Given the following regular hexagon
We know that the length of one side of the hexagon is $5$ cm.
Find the area of the regular hexagon.

Solution:
We will proceed according to the formula and set $a=5$. We will obtain:
$6\times\frac{5^2 \sqrt3}{4}=64.95$

The area of the regular hexagon is $64.95$ cm².

For more information on the area of the regular hexagon click here