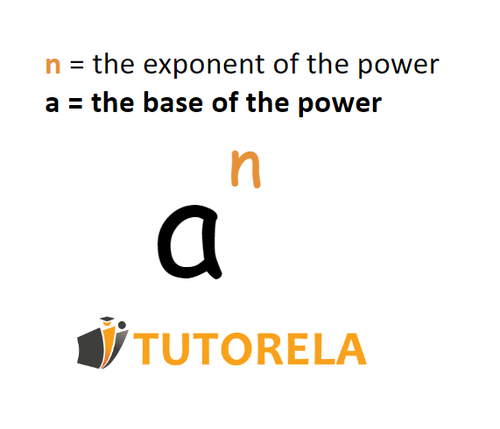
Which of the following is equivalent to the expression below?
10,0001
To solve this problem, we will apply the rule of exponents:
- Any number raised to the power of 1 remains unchanged. Therefore, by the identity property of exponents, 10,0001=10,000.
Given the choices:
- 10,000⋅10,000: This is 10,0002.
- 10,000⋅1: Simplifying this expression yields 10,000, which is equivalent to 10,0001.
- 10,000+10,000: This results in 20,000, not equivalent to 10,0001.
- 10,000−10,000: This results in 0, not equivalent to 10,0001.
Therefore, the correct choice is 10,000⋅1, which simplifies to 10,000, making it equivalent to 10,0001.
Thus, the expression 10,0001 is equivalent to:
10,000⋅1
10,000⋅1