Using the Pythagorean Theorem: Applying the formula

What is the length of the hypotenuse?

We use the Pythagorean theorem

$AC^2+AB^2=BC^2$

We insert the known data:

$3^2+4^2=BC^2$

$9+16=BC^2$

$25=BC^2$

We extract the root:

$\sqrt{25}=BC$

$5=BC$

5

Look at the triangle in the diagram. Calculate the length of side AC.

To solve the exercise, we have to use the Pythagorean theorem:

A²+B²=C²

We replace the data we have:

3²+4²=C²

9+16=C²

25=C²

5=C

5 cm

Look at the triangle in the diagram. How long is side AB?

To find side AB, we will need to use the Pythagorean theorem.

The Pythagorean theorem allows us to find the third side of a right triangle, if we have the other two sides.

You can read all about the theorem here.

Pythagorean theorem:

$A^2+B^2=C^2$

That is, one side squared plus the second side squared equals the third side squared.

We replace the existing data:

$3^2+2^2=AB^2$

$9+4=AB^2$

$13=AB^2$

We find the root:

$\sqrt{13}=AB$

$\sqrt{13}$ cm

Look at the triangle in the diagram. How long is side BC?

To solve the exercise, it is necessary to know the Pythagorean Theorem:

A²+B²=C²

We replace the known data:

2²+B²=7²

4+B²=49

We input into the formula:

B²=49-4

B²=45

We find the root

B=√45

This is the solution. However, we can simplify the root a bit more.

First, let's break it down into prime numbers:

B=√(9*5)

We use the property of roots in multiplication: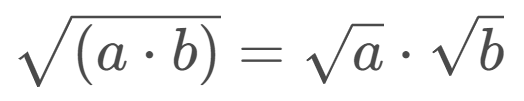

B=√9*√5

B=3√5

This is the solution!

$3\sqrt{5}$ cm

Given the triangle ABC, find the length BC

To answer this question, we must know the Pythagorean Theorem

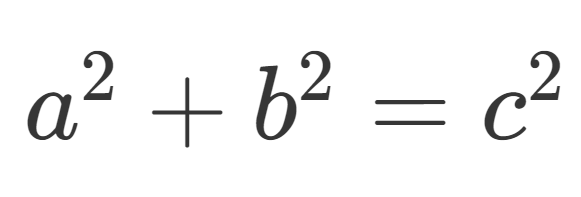
The theorem allows us to calculate the sides of a right triangle.

We identify the sides:

ab = a = 5
bc = b = ?

ac = c = 13

We replace the data in the exercise:

5²+?² = 13²

We swap the sections

?²=13²-5²

?²=169-25

?²=144

?=12

12 cm

Calculate AE given that triangle ABC is isosceles.

$8\frac{1}{3}$

A cuboid has a width measuring 8 cm and a height of 4 cm.

Calculate the length of the side AC.

$\sqrt{80}$ cm