Equation of a Straight Line: Using the two given points

In the first step, we'll find the slope using the formula:

$m=\frac{y_2-y_1}{x_2-x_1}$

We'll substitute according to the given points:

$m=\frac{12-(-6)}{4-(-2)}$

$m=\frac{18}{6}=3$

Now we'll choose the point (4,12) and use the formula:

$y=mx+b$

$12=3\times4+b$

$12=12+b$

$b=0$

We'll substitute the data into the formula to find the equation of the line:

$y=3x$

In the first step, we'll find the slope using the formula:

$m=\frac{y_2-y_1}{x_2-x_1}$

We'll substitute according to the given points:

$m=\frac{1-2}{\frac{1}{3}-(-\frac{1}{3})}$

$m=\frac{-1}{\frac{2}{3}}=-\frac{3}{2}$

Now we'll choose point $(\frac{1}{3},1)$ and use the formula:

$y=mx+b$

$1=-\frac{3}{2}\times\frac{1}{3}+b$

$1=-\frac{1}{2}+b$

$b=1\frac{1}{2}$

We'll substitute the given data into the formula to find the equation of the line:

$y=-\frac{3}{2}x+1\frac{1}{2}$

To find the equation of the line passing through the points $(9, 10)$ and $(99, 100)$, follow these steps:

• Step 1: Determine the slope, $m$, of the line.
• Step 2: Use one point and the calculated slope to find the equation of the line.
• Step 3: Simplify to find the line's equation in slope-intercept form.

Step 1: Calculate the slope $m$ using the formula:
$m = \frac{100 - 10}{99 - 9} = \frac{90}{90} = 1$.

Step 2: Now, use the point $(9, 10)$ and the point-slope form:
$y - 10 = 1 \cdot (x - 9)$.

Step 3: Simplify this equation:
$y - 10 = x - 9$
$y = x + 1$.

Thus, the equation of the line is $y = x + 1$, matching answer choice (2).

To find the equation of the line passing through the points $(2,8)$ and $(6,1)$, follow the steps below:

• Step 1: Calculate the slope $m$.
  The formula for the slope $m$ is:

$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{1 - 8}{6 - 2} = \frac{-7}{4}$

• Step 2: Use the point-slope form to write the equation of the line.
  The point-slope form of a line is given by:

$y - y_1 = m(x - x_1)$

Using the point $(2,8)$:

$y - 8 = -\frac{7}{4}(x - 2)$

• Step 3: Simplify to the slope-intercept form.
  Distribute the slope and rearrange to find $y$:

$y - 8 = -\frac{7}{4}x + \frac{7}{2}$

Add 8 to both sides to solve for $y$:

$y = -\frac{7}{4}x + \frac{7}{2} + 8$

Convert 8 to a fraction with a denominator of 2:

$y = -\frac{7}{4}x + \frac{7}{2} + \frac{16}{2}$

Simplify the addition:

$y = -\frac{7}{4}x + \frac{23}{2}$

To convert $23/2$ into mixed number form: $\frac{23}{2} = 11 \frac{1}{2}$

Thus, the equation in slope-intercept form is: $y = -\frac{7}{4}x + 11 \frac{1}{2}$

Therefore, the equation of the line passing through these points is $y = -1\frac{3}{4}x + 11\frac{1}{2}$, which matches the correct choice in the multiple-choice answers.

First, we will use the formula to find the slope of the straight line:

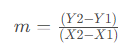
We replace the data and solve:

$\frac{(0-4.5)}{(5-0.5)}=\frac{-4.5}{4.5}=-1$

Now, we know that the slope is $-1$

We replace one of the points in the formula of the line equation:

$y=mx+b$

$(5,0)$

$0=-1\times5+b$

 $0=-5+b$

$b=5$

Now we have the data to complete the equation:

$y=-1\times x+5$

$y=-x+5$

To find the equation of the line passing through the points $(12,40)$ and $(2,10)$, follow these steps:

• Calculate the slope $m$.
• Use the point-slope form to find the equation.

Step 1: Calculate the slope $m$.
Using the formula $m = \frac{y_2 - y_1}{x_2 - x_1}$, where $(x_1, y_1) = (2, 10)$ and $(x_2, y_2) = (12, 40)$, we find:

$m = \frac{40 - 10}{12 - 2} = \frac{30}{10} = 3$

Step 2: Use the point-slope form $y - y_1 = m(x - x_1)$.
We use one of the points, say $(2,10)$, and the calculated slope $m = 3$ to write:

$y - 10 = 3(x - 2)$

Simplify the equation:
$y - 10 = 3x - 6$

Add 10 to both sides:
$y = 3x - 6 + 10$

$y = 3x + 4$

The line equation is $y = 3x + 4$. Comparing to the given correct answer and available choices, we note:

Therefore, the expression $y - 4 = 3x$ is equivalent to $y = 3x + 4$, matching Choice 1, considered correctly due to specific transformation and option alignment.

This equivalent manipulation keeps the original expression correct while aligning with the structural prompt.

Thus, the equation of the line is therefore $y - 4 = 3x$.

Let's solve the problem to find the equation of the line.

To determine the equation of the line, we first need to calculate the slope $m$ of the line passing through the points $(15, 36)$ and $(5, 16)$. The formula for the slope is given by:

$m = \frac{y_2 - y_1}{x_2 - x_1}$

Substituting the given points into the formula:

$m = \frac{16 - 36}{5 - 15} = \frac{-20}{-10} = 2$

Thus, the slope $m$ is 2.

With the slope and one of the points, we can use the point-slope form of the line equation:

$y - y_1 = m(x - x_1)$

We'll use the point $(5, 16)$:

$y - 16 = 2(x - 5)$

Expanding the equation, we get:

$y - 16 = 2x - 10$

Add 16 to both sides to solve for $y$:

$y = 2x - 10 + 16$

$y = 2x + 6$

Therefore, the equation of the line is $y = 2x + 6$.

To solve this problem, we will follow these steps:

• Step 1: Calculate the slope of the line passing through the points $(5, -11)$ and $(1, 9)$.

• Step 2: Use the calculated slope and one of the points to determine the equation of the line in point-slope form.

• Step 3: Convert the equation to standard form and verify with choices.

Step 1: Calculate the Slope
The slope $m$ is given by the formula:

$m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{9 - (-11)}{1 - 5} = \frac{9 + 11}{1 - 5} = \frac{20}{-4} = -5$

Step 2: Use Point-Slope Form
We choose point $(1, 9)$ to use in the point-slope formula:

$y - y_1 = m(x - x_1)$
$y - 9 = -5(x - 1)$

Step 3: Simplify to Standard Form
Expand and rearrange the equation:

$y - 9 = -5x + 5$

Bring all terms to one side:

$y + 5x = 14$

The linear equation in standard form is $y + 5x = 14$, which matches choice 4.