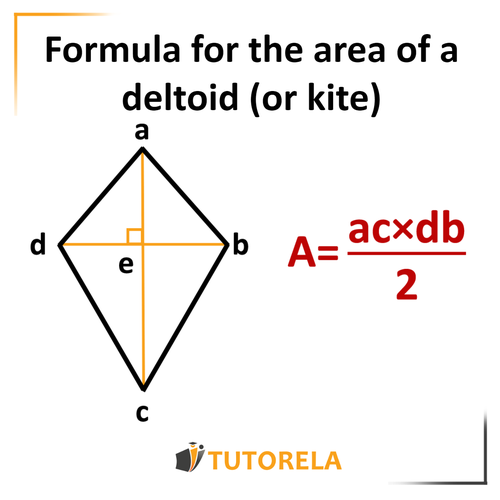
The area of the kite can be calculated by multiplying the lengths of the diagonals and dividing this product by .
Area of a Deltoid - Examples, Exercises and Solutions
How do we calculate the area of a kite?
Deltoid Area Formula
To facilitate the understanding of the concept of calculus, you can use the following drawing and the accompanying formula:
Practice Area of a Deltoid
Look at the deltoid in the figure:
What is its area?
Look at the deltoid in the figure:
What is its area?
ACBD is a deltoid.
AD = AB
CA = CB
Given in cm:
AB = 6
CD = 10
Calculate the area of the deltoid.
ABDC is a deltoid.
AB = BD
DC = CA
AD = 12 cm
CB = 16 cm
Calculate the area of the deltoid.
Shown below is the deltoid ABCD.
The diagonal AC is 8 cm long.
The area of the deltoid is 32 cm².
Calculate the diagonal DB.
Examples with solutions for Area of a Deltoid
Exercise #1
Look at the deltoid in the figure:
What is its area?
Video Solution
Step-by-Step Solution
Let's begin by reminding ourselves of the formula for the area of a kite
Both these values are given to us in the figure thus we can insert them directly into the formula:
(4*7)/2
28/2
14
Answer
14
Exercise #2
Look at the deltoid in the figure:
What is its area?
Video Solution
Step-by-Step Solution
To solve the exercise, we first need to know the formula for calculating the area of a kite:

It's also important to know that a concave kite, like the one in the question, has one of its diagonals outside the shape, but it's still its diagonal.
Let's now substitute the data from the question into the formula:
(6*5)/2=
30/2=
15
Answer
15
Exercise #3
ACBD is a deltoid.
AD = AB
CA = CB
Given in cm:
AB = 6
CD = 10
Calculate the area of the deltoid.
Video Solution
Step-by-Step Solution
To solve the exercise, we first need to remember how to calculate the area of a rhombus:
(diagonal * diagonal) divided by 2
Let's plug in the data we have from the question
10*6=60
60/2=30
And that's the solution!
Answer
30
Exercise #4
ABDC is a deltoid.
AB = BD
DC = CA
AD = 12 cm
CB = 16 cm
Calculate the area of the deltoid.
Video Solution
Step-by-Step Solution
First, let's recall the formula for the area of a rhombus:
(Diagonal 1 * Diagonal 2) divided by 2
Now we will substitute the known data into the formula, giving us the answer:
(12*16)/2
192/2=
96
Answer
96 cm²
Exercise #5
Shown below is the deltoid ABCD.
The diagonal AC is 8 cm long.
The area of the deltoid is 32 cm².
Calculate the diagonal DB.
Video Solution
Step-by-Step Solution
First, we recall the formula for the area of a kite: multiply the lengths of the diagonals by each other and divide the product by 2.
We substitute the known data into the formula:
We reduce the 8 and the 2:
Divide by 4
Answer
8 cm
The deltoid below has an area of 60 cm².
What is the value of X?
The kite ABCD shown below has an area of 42 cm².
AB = BC
DC = AD
BD = 14
The diagonals of the kite intersect at point 0.
Calculate the length of side AO.
Given the deltoid ABCD
The main diagonal is equal to 2a+2
Secondary diagonal is equal to a
The area of the deltoid equals 6a
Calculate a a
A deltoid-shaped stage is to be built in a rectangular field.
The length of the field is 30 m and the width is 20 m.
Determine the area of the stage shaded in orange?
Below is a deltoid with a length 2 times its width and an area equal to 16 cm².
Calculate x.
Exercise #6
The deltoid below has an area of 60 cm².
What is the value of X?
Video Solution
Step-by-Step Solution
To solve the problem, we need to remember the formula for the area of a rhombus:
The product of the diagonals multiplied together and then divided by 2.
Let's substitute in our data into the formula:
(8*X) = 60
2
Note that we can simplify the fraction, thus eliminating the denominator:
4X = 60
Let's finally divide the equation by 4 to get our answer:
X = 15
Answer
15
Exercise #7
The kite ABCD shown below has an area of 42 cm².
AB = BC
DC = AD
BD = 14
The diagonals of the kite intersect at point 0.
Calculate the length of side AO.
Video Solution
Step-by-Step Solution
We substitute the data we have into the formula for the area of the kite:
We multiply by 2 to remove the denominator:
Then divide by 14:
In a rhombus, the main diagonal crosses the second diagonal, therefore:
Answer
3 cm
Exercise #8
Given the deltoid ABCD
The main diagonal is equal to 2a+2
Secondary diagonal is equal to a
The area of the deltoid equals 6a
Calculate a a
Video Solution
Step-by-Step Solution
To solve the question, we first need to remember the formula for the area of a kite:
Diagonal * Diagonal / 2
This means that if we substitute the given data we can see that:
a(2a+2)/2 = area of the kite
Let's remember that we are also given the area, so we'll put that in the equation too
a(2a+2)/2 = 6a
Now we have an equation that we can easily solve.
First, let's get rid of the fraction, so we'll multiply both sides of the equation by 2
a(2a+2)=6a*2
a(2a+2)=12a
Let's expand the parentheses on the left side of the equation
2a²+2a=12a
2a²=10a
Let's divide both sides of the equation by a
2a=10
Let's divide again by 2
a=5
And that's the solution!
Answer
5 cm
Exercise #9
A deltoid-shaped stage is to be built in a rectangular field.
The length of the field is 30 m and the width is 20 m.
Determine the area of the stage shaded in orange?
Video Solution
Step-by-Step Solution
We can calculate the area of rectangle ABCD as follows:
Now let's divide the deltoid along its length and width and add the following points:
Finally, we can calculate the area of deltoid PMNK as follows:
Answer
300 m
Exercise #10
Below is a deltoid with a length 2 times its width and an area equal to 16 cm².
Calculate x.
Video Solution
Step-by-Step Solution
Given the problem, we are tasked to find the value of for a deltoid where the length is twice the width and the area is given. Let's proceed as follows:
- Step 1: In this deltoid problem, the diagonals correspond to length and width . The formula for the area of a deltoid in terms of its diagonals is .
- Step 2: Substitute the values. Thus, the area .
- Step 3: Simplify the equation: .
- Step 4: Solve for : We find , so .
- Step 5: Conclude .
Therefore, the solution to the problem is .
Answer
Look at the kite ABCD below.
Diagonal DB = 10
CB = 4
Is it possible to calculate the area of the kite? If so, what is it?
Given the deltoid ABCD
Find the area
Given the deltoid ABCD
Find the area
Given the deltoid ABCD
Find the area
Given the deltoid ABCD
Find the area
Exercise #11
Look at the kite ABCD below.
Diagonal DB = 10
CB = 4
Is it possible to calculate the area of the kite? If so, what is it?
Video Solution
Answer
It is not possible.
Exercise #12
Given the deltoid ABCD
Find the area
Video Solution
Answer
cm².
Exercise #13
Given the deltoid ABCD
Find the area
Video Solution
Answer
cm².
Exercise #14
Given the deltoid ABCD
Find the area
Video Solution
Answer
cm².
Exercise #15
Given the deltoid ABCD
Find the area
Video Solution
Answer
cm².