A percentage is a number that expresses a part of .
Quantity refers to the absolute number of something.
The percentage value refers to the quantity that corresponds to the specific percentage of the whole.
Percentage Practice Problems & Word Problems with Solutions
Master percentage calculations with step-by-step practice problems. Learn to find percentage values, convert percentages to numbers, and solve real-world applications.
- Calculate percentage values using the fundamental percentage formula
- Convert percentages to actual numbers in real-world scenarios
- Find what percentage one number is of another
- Determine total quantities when given percentage and percentage value
- Solve discount and price reduction percentage problems
- Apply percentage concepts to classroom and everyday situations
Understanding Percentage
What is a percentage?
In order to solve questions about finding the quantity, percentage and percentage value, we use the following equation:
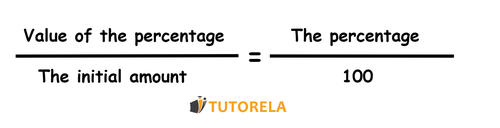
We will always have given values and one unknown that we need to determine.
Pay attention - The data in the question doesn't always direct us to what we're being asked. Therefore, we'll need to use logic and select the values that will provide us with the correct answer.
Practice Percentage
Calculate 8% of 100:
Examples with solutions for Percentage
Calculate 30 over 100 as a percentage:
In order to determine what percentage 30 is out of 100, you can use the following formula:
We begin by substituting the given values into the formula:
We then proceed to simplify the expression:
Therefore, 30 out of 100 is 30%.
Answer:
30%
Calculate 3% of 100:
To solve this problem, we'll proceed with the following steps:
- Step 1: Identify the given information
We are given a percentage of 3% and a whole number of 100. - Step 2: Use the percentage formula
The formula to calculate the percentage of a whole number is given by:
- Step 3: Substitute the values and calculate
Substituting the given values into the formula, we have:
Therefore, the 3% of 100 is .
Answer:
3
Calculate 32 over 100 as a percentage:
To solve this problem, we'll follow these steps:
- Step 1: Identify the given fraction .
- Step 2: Recognize that the denominator of 100 aligns directly with the meaning of percentage.
- Step 3: Conclude that when the fraction is , it equals .
Now, let's work through each step:
Step 1: The problem gives us the fraction .
Step 2: Since the denominator is 100, the fraction directly represents a percentage.
Step 3: This means that is simply .
Therefore, the solution to the problem is .
Answer:
32%
Calculate 25 over 100 as a percentage:
In order to determine what percentage 25 is out of 100, we use the following formula:
.
We begin by substituting in the known values:
.
Thus, 25 out of 100 is .
Answer:
25%
Calculate 40 over 100 as a percentage:
In order to determine what percentage 40 is out of 100, we use the following formula:
We begin by substituting in the known values:
We then proceed to solve the expression:
Thus, 40 out of 100 is 40%.
Answer:
40%