Prime factorization (or prime decomposition) consists of breaking down a certain number into prime numbers, called factors, whose product (multiplication) results in the original number.
Prime Factorization Practice Problems & Worksheets
Master prime factorization with step-by-step practice problems. Learn factor tree method and division method to decompose numbers into prime factors.
- Apply the factor tree method to break down composite numbers systematically
- Use the split-window division method to find prime factors efficiently
- Identify prime and composite numbers to determine factorization endpoints
- Verify prime factorization results by multiplying factors back to original numbers
- Compare different factorization paths to reach the same prime factor result
- Solve multi-step problems involving prime decomposition of larger numbers
Understanding Prime Factorization
Prime Factorization
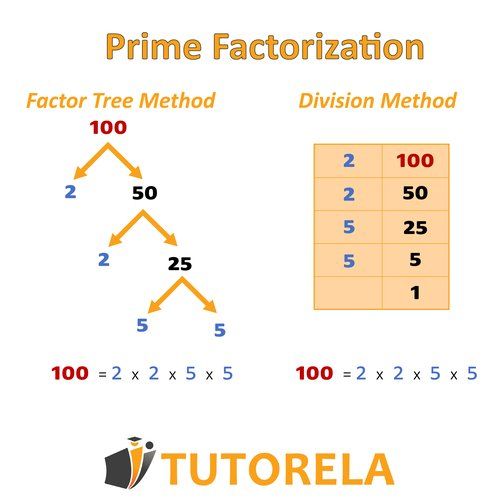
The first method - Factor tree method
Let's take the number we want to factorize and draw branches from it.
We will ask ourselves, which numbers can we find whose multiplication results in this same number, except for the original number and .
Let's see if the numbers we found are prime or composite, we will break down the composite ones into two branches again.
We will continue breaking down all the composite numbers until we only have primes, which we will mark with a circle.
The second method - Split Window Method
Let's write the number we want to factorize on the left side of a vertical line that acts as a division window.
Let's look for the smallest prime number by which we can divide the original, we write it on the right side of the line and the result we write on the left, below the first one. We will continue in this manner until we reach the number and finish the exercise.
All the prime numbers will appear on the right side of the dividing line.
Practice Prime Factorization
Write all the factors of the following number: \( 290 \)
Examples with solutions for Prime Factorization
Write the prime factors of the following number:
To solve this problem, we'll follow these steps:
- Identify all the factors of the number 4.
- Determine which of these factors are prime numbers.
- Check the answer choices to find the one that corresponds to the prime factorization of 4.
Now, let's work through each step:
Step 1: To find the factors of 4, we consider pairs of numbers that multiply to 4, such as and .
Step 2: Among these factors, identify the prime numbers. The number 2 is the only prime factor, and it needs to be listed twice since .
Step 3: Looking at the answer choices, the choice that corresponds to the prime factorization of 4 is .
Therefore, the correct answer is .
Answer:
Write all the factors of the following number:
To determine the factors of the number , we will follow these steps:
Step 1: Begin by checking each number starting from up to to see if it divides evenly.
Step 2: Check . Since , is a factor.
Step 3: Check . Since , is a factor.
Step 4: Check . Since , is a factor.
Step 5: Check . Since is not evenly divisible by , is not a factor.
Step 6: Check . Since is not evenly divisible by , is not a factor.
Step 7: Finally, check . Since , is a factor.
All possible whole number products (pairs) that result in are , , , and .
However, when checking for unique prime factors as a particular approach in factors identification, breaks down into prime factors of and .
Therefore, the primary distinct prime factors of are and .
This correlates with choice 3:
Choice : , which matches our factors.
Thus, the answer is correctly represented as the distinct prime factors in the context of the problem requirements.
Answer:
Write all the factors of the following number:
To determine all the factors of the number 7, we will examine which integers between 1 and 7 divide it exactly:
- Check 1: Since , 1 is a factor.
- Check 2: , which is not an integer, so 2 is not a factor.
- Check 3: , which is not an integer, so 3 is not a factor.
- Check 4: , which is not an integer, so 4 is not a factor.
- Check 5: , which is not an integer, so 5 is not a factor.
- Check 6: , which is not an integer, so 6 is not a factor.
- Check 7: Since , 7 is a factor.
Therefore, the factors of 7 are and .
These results correspond to choice 1: .
Answer:
No prime factors
Write all the factors of the following number:
To find all the factors of 9, we will determine the divisors of the number 9 by testing each integer from 1 up to 9.
- Step 1: Test if 1 is a factor of 9. Since , 1 is a factor.
- Step 2: Test if 2 is a factor of 9. Since (not an integer), 2 is not a factor.
- Step 3: Test if 3 is a factor of 9. Since , 3 is a factor.
- Step 4: Test if 4 is a factor of 9. Since (not an integer), 4 is not a factor.
- Step 5: Test if 5 is a factor of 9. Since (not an integer), 5 is not a factor.
- Step 6: Test if 6 is a factor of 9. Since (not an integer), 6 is not a factor.
- Step 7: Test if 7 is a factor of 9. Since (not an integer), 7 is not a factor.
- Step 8: Test if 8 is a factor of 9. Since (not an integer), 8 is not a factor.
- Step 9: Test if 9 is a factor of 9. Since , 9 is a factor.
The factors of 9 are 1, 3, and 9.
However, the problem might specifically be asking for the prime factorization where the number 9 decomposes into .
Therefore, the correct answer which matches the provided choices is .
Answer:
Write all the factors of the following number:
To find the factors of 8, we'll use prime factorization.
- Step 1: Begin with the smallest prime number, 2.
- Step 2: Divide 8 by 2, which gives 4. Since 4 is even, divide by 2 again.
- Step 3: Divide 4 by 2, which gives 2. Divide 2 by 2 one more time.
- Step 4: This yields 1, so we've fully factored the number.
Thus, the prime factorization of 8 is .
The factors of the number 8 are .
Therefore, the correct answer is choice 4: .
Answer: