Prime factorization (or prime decomposition) consists of breaking down a certain number into prime numbers, called factors, whose product (multiplication) results in the original number.
Prime Factorization
Prime Factorization
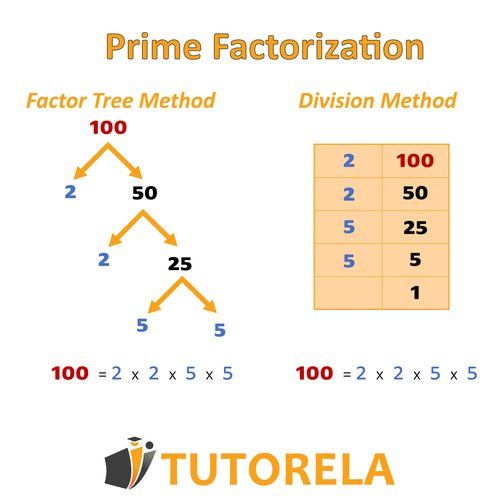
The first method - Factor tree method
Let's take the number we want to factorize and draw branches from it.
We will ask ourselves, which numbers can we find whose multiplication results in this same number, except for the original number and .
Let's see if the numbers we found are prime or composite, we will break down the composite ones into two branches again.
We will continue breaking down all the composite numbers until we only have primes, which we will mark with a circle.
The second method - Split Window Method
Let's write the number we want to factorize on the left side of a vertical line that acts as a division window.
Let's look for the smallest prime number by which we can divide the original, we write it on the right side of the line and the result we write on the left, below the first one. We will continue in this manner until we reach the number and finish the exercise.
All the prime numbers will appear on the right side of the dividing line.
Test yourself on prime factorization!
Write all the factors of the following number: \( 6 \)
Prime Factorization
In this article, you will learn to break down any number into prime factors with the help of two magnificent tricks that you will surely love!
What is factor decomposition (or factorization)?
Factor decomposition (factorization or prime factorization) is the decomposition of a certain number into smaller numbers - primes, whose product (multiplication) is the original number.
After having learned what a composite number and a prime number are, we will learn here how to decompose a composite number into prime factors.
Write all the factors of the following number: \( 7 \)
Write all the factors of the following number: \( 5 \)
Write all the factors of the following number: \( 9 \)
The first method - Factor Tree Method
We will take the number we want to factorize and draw branches from it.
For example:

We will ask ourselves, which numbers can we find whose multiplication results in this same number, except for the original number and .
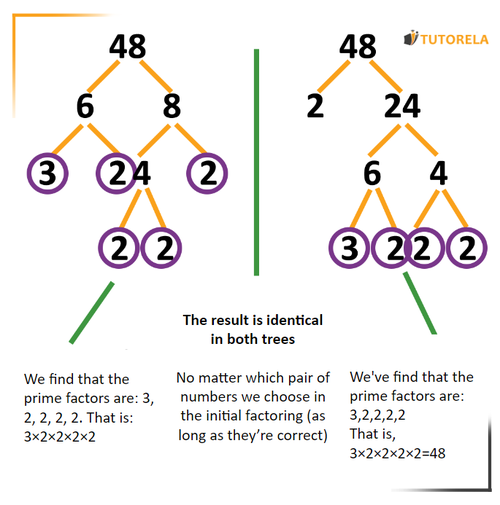
In this example, we will choose the numbers and .
Note that, we could have chosen any pair of numbers whose product was and, anyway, we would have arrived at the same result.
We will write the and the under the branches as follows:
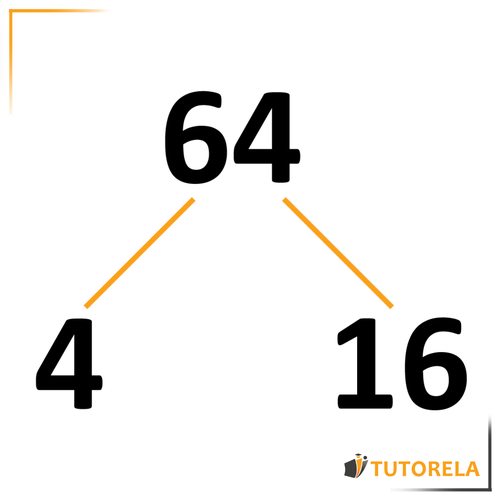
Now we will find out if and are composite numbers. Again, we will look for numbers whose product is or .
Attention! This is valid except for the number itself and .
For the number , we can find and
For the number , we can find and
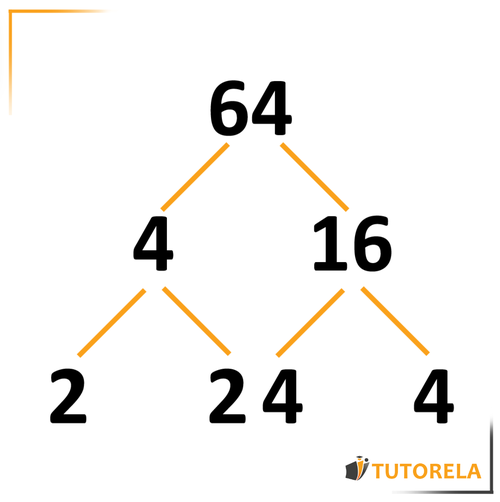
Again, we will extract roots from each number and write the factors in the following way:
Now we will continue asking
Is a prime number?
Yes.
Is a prime number?
No. We can continue factoring out and .
Therefore, we will continue with the tree on the right side and circle all the factors that are prime numbers.
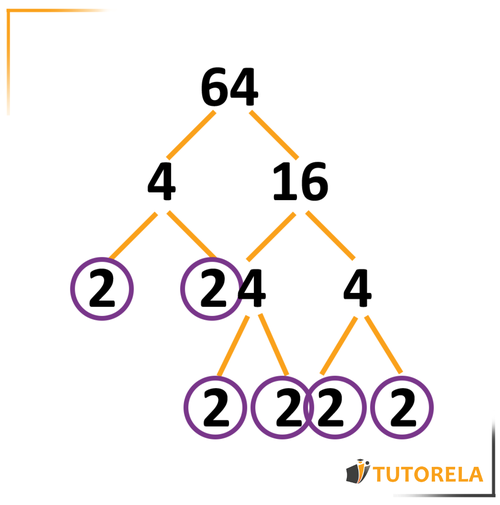
What do we get?
If we break down into its prime factors, we will find that:
are the prime factors of .
Another example
Let's take the number and see how we arrive at the same result even if we start breaking it down with different factors:
On the right, we will break down as the product of and . On the left, we will break down as the product of and .
We will continue according to the operation steps
On the right, we will only break down . is prime, therefore, we will mark it with a circle.
On the left, we will break down and also .
We will continue breaking down all composite numbers until we only have primes, which we will mark with a circle.
Write all the factors of the following number: \( 8 \)
Write the prime factors of the following number: \( 4 \)
Write all the factors of the following number: \( 16 \)
The second method: Split-window division method
Let's write the number we want to factorize on the left side of a vertical line that acts as a division window.
Let's look for the smallest prime number by which we can divide the original, we write it on the right side of the line and the result we write on the left, below the first one. We will continue in this way until we reach the number and finish the exercise.
All the prime numbers will appear on the right side of the dividing line.
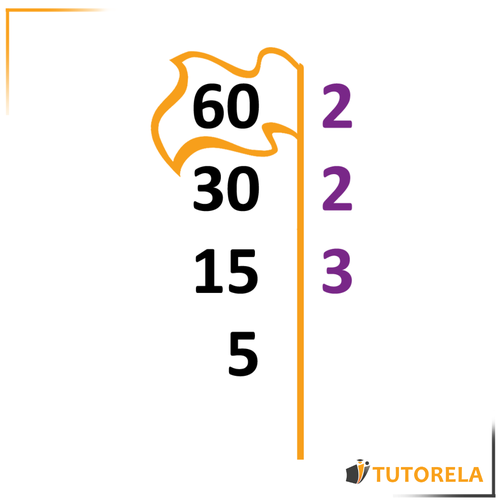
Let's see it in practice: We will break down the number into prime factors:
We will ask ourselves, what is the smallest prime number by which we can divide it? The answer is . is a prime number and is divisible by it.
We will write next to the number to the right of the division line.
Let's calculate
We will write the quotient (result of the division) below the original number, as follows:

Now, we will continue questioning: What is the smallest prime number that divides ?
The answer is .
We will write on the right again and note the quotient on the left:

Now, we will continue asking: What is the smallest prime number that divides ?
The answer is . We will write it to the right and the quotient to the left.
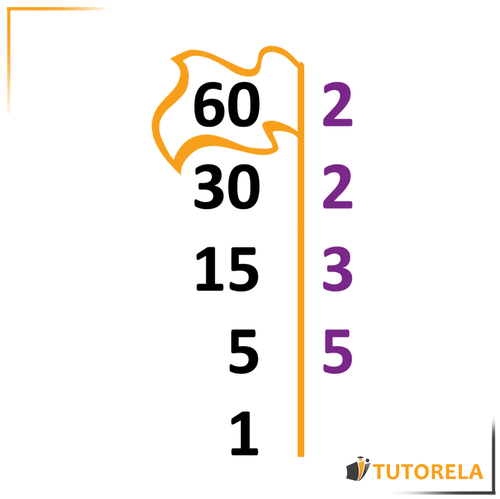
Now, we will continue questioning: What is the smallest prime number that divides ?
The answer is .
We will note it on the right and the result on the left.
We have reached the number , which cannot be factored further.
That means we have finished the exercise and the prime factors are those that appear on the right side.
That is:
Examples and exercises with solutions for prime factorization
Exercise #1
Write all the factors of the following number:
Video Solution
Step-by-Step Solution
To determine the factors of the number , we will follow these steps:
Step 1: Begin by checking each number starting from up to to see if it divides evenly.
Step 2: Check . Since , is a factor.
Step 3: Check . Since , is a factor.
Step 4: Check . Since , is a factor.
Step 5: Check . Since is not evenly divisible by , is not a factor.
Step 6: Check . Since is not evenly divisible by , is not a factor.
Step 7: Finally, check . Since , is a factor.
All possible whole number products (pairs) that result in are , , , and .
However, when checking for unique prime factors as a particular approach in factors identification, breaks down into prime factors of and .
Therefore, the primary distinct prime factors of are and .
This correlates with choice 3:
Choice : , which matches our factors.
Thus, the answer is correctly represented as the distinct prime factors in the context of the problem requirements.
Answer
Exercise #2
Write all the factors of the following number:
Video Solution
Step-by-Step Solution
To determine all the factors of the number 7, we will examine which integers between 1 and 7 divide it exactly:
- Check 1: Since , 1 is a factor.
- Check 2: , which is not an integer, so 2 is not a factor.
- Check 3: , which is not an integer, so 3 is not a factor.
- Check 4: , which is not an integer, so 4 is not a factor.
- Check 5: , which is not an integer, so 5 is not a factor.
- Check 6: , which is not an integer, so 6 is not a factor.
- Check 7: Since , 7 is a factor.
Therefore, the factors of 7 are and .
These results correspond to choice 1: .
Answer
No prime factors
Exercise #3
Write all the factors of the following number:
Video Solution
Step-by-Step Solution
To find all the factors of 9, we will determine the divisors of the number 9 by testing each integer from 1 up to 9.
- Step 1: Test if 1 is a factor of 9. Since , 1 is a factor.
- Step 2: Test if 2 is a factor of 9. Since (not an integer), 2 is not a factor.
- Step 3: Test if 3 is a factor of 9. Since , 3 is a factor.
- Step 4: Test if 4 is a factor of 9. Since (not an integer), 4 is not a factor.
- Step 5: Test if 5 is a factor of 9. Since (not an integer), 5 is not a factor.
- Step 6: Test if 6 is a factor of 9. Since (not an integer), 6 is not a factor.
- Step 7: Test if 7 is a factor of 9. Since (not an integer), 7 is not a factor.
- Step 8: Test if 8 is a factor of 9. Since (not an integer), 8 is not a factor.
- Step 9: Test if 9 is a factor of 9. Since , 9 is a factor.
The factors of 9 are 1, 3, and 9.
However, the problem might specifically be asking for the prime factorization where the number 9 decomposes into .
Therefore, the correct answer which matches the provided choices is .
Answer
Exercise #4
Write all the factors of the following number:
Video Solution
Step-by-Step Solution
To find the factors of 8, we'll use prime factorization.
- Step 1: Begin with the smallest prime number, 2.
- Step 2: Divide 8 by 2, which gives 4. Since 4 is even, divide by 2 again.
- Step 3: Divide 4 by 2, which gives 2. Divide 2 by 2 one more time.
- Step 4: This yields 1, so we've fully factored the number.
Thus, the prime factorization of 8 is .
The factors of the number 8 are .
Therefore, the correct answer is choice 4: .
Answer
Exercise #5
Write the prime factors of the following number:
Video Solution
Step-by-Step Solution
To solve this problem, we'll follow these steps:
- Identify all the factors of the number 4.
- Determine which of these factors are prime numbers.
- Check the answer choices to find the one that corresponds to the prime factorization of 4.
Now, let's work through each step:
Step 1: To find the factors of 4, we consider pairs of numbers that multiply to 4, such as and .
Step 2: Among these factors, identify the prime numbers. The number 2 is the only prime factor, and it needs to be listed twice since .
Step 3: Looking at the answer choices, the choice that corresponds to the prime factorization of 4 is .
Therefore, the correct answer is .
Answer
Write all the factors of the following number: \( 12 \)
Write all the factors of the following number: \( 13 \)
Write all the factors of the following number: \( 14 \)









