A consecutive number is a number that is 1 greater than the existing number.
For example:
The consecutive number of is:
The answer is
Magnitude in the hundreds range
Magnitude in the hundreds range
Consecutive numbers
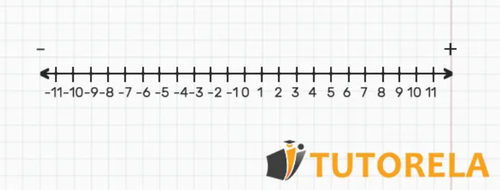
number line
A number line is an infinite line without an end and without a beginning on which numbers are located.
The line is divided into equal intervals or segments that are identical in size and each interval is the distance between two equal numbers.
On the line there are small lines called marks.
As we move right - the numbers get larger
As we move left - the numbers get smaller
Sequences and Skips
An arithmetic sequence is a sequence of numbers that follow one another with equal intervals between them.
The sequence can increase and the sequence can also decrease.
We always read the sequence from left to right! Just like reading a number.
If the first number is smaller than the last number - there is an increase - ascending sequence
If the first number is larger than the last number - there is a decrease - descending sequence
Magnitude in the hundreds range
Consecutive numbers
A consecutive number is a number that is greater than the existing number by 1.
When we are asked -
The consecutive number of "any number" is...
We calculate as follows:
For example:
The consecutive number of is:
The answer is
When we are asked -
"Some number" is the consecutive number of...
We calculate as follows:
For example:
is the consecutive number of:
The answer is
Consecutive numbers sequence
Consecutive numbers from smallest to largest are numbers that follow one another in ascending order,
for example:
Sum of Consecutive Numbers
The sum of consecutive numbers is the addition of all consecutive numbers in the exercise
For example -
Determine the sum of the consecutive numbers in the exercise:
We add together all the numbers:
We can use the commutative and associative properties and calculate as shown below:
The sum of consecutive numbers in the exercise is .
Number Line
What is a number line?
A number line is an infinite line without an end and without a beginning on which numbers are located.
The line is divided into equal intervals or segments that are identical in size, and each interval is the distance between two equal numbers.
On the line there are small lines called marks.
As we move right - the numbers get larger
As we move left - the numbers get smaller
In order to complete missing numbers on a number line, we follow these steps:
- Find the number of arcs between one mark to another – understand how many jumps there are.
- Divide the "final" number on the number line by the number of arcs.
- Starting from , add the interval we found each time to find all the numbers on the line.
Note - an interval is the part between each tick mark. Even if the number is on a tick mark, the jump to it is called an interval.
Let's practice!
Complete the missing numbers:

Solution:
Note that we have types of marks - some long and some short.
First, let's find the missing number at the long mark -
There are two intervals between the long marks, therefore
The second missing number is
Now let's look at the small marks:
In the first part, there is 1 small mark that creates two intervals.
Therefore we calculate as follows:
The first missing number is .
Now we need to understand what is the difference between the final number and - the second missing number we found.
We get:
Now let's understand how many intervals we have between and :
Let's count and we can determine that there are intervals.
Now let's divide the difference by the number of intervals and we obtain the following answer:
The interval between the small marks is
therefore the third missing number will be:
The answer is
Sequences and Skips
An arithmetic sequence is a sequence of numbers that follow one another with equal intervals between them.
The sequence can increase and the sequence can also decrease.
We always read the sequence from left to right! Exactly like reading a number.
If the first number is smaller than the last number - there is an increase - increasing sequence
If the first number is larger than the last number - there is a decrease - decreasing sequence
To discover the pattern of a sequence, we ask:
In which digit did the change occur? Ones/tens/hundreds/thousands
When we know which digit changed, we can immediately identify the intervals between numbers and discover the pattern - addition or subtraction of...
Exercise:
Complete the following sequence,
determine if it is increasing or decreasing and find its pattern.
Solution:
First, let's determine if the sequence is increasing or decreasing.
The first number in the sequence is
The last number is
There is a decrease, therefore the sequence is decreasing
Let's examine in which digit the change occurs - the change occurs in the tens digit.
Every numbers, the number decreases by .
Therefore, the pattern is - subtraction of .
Now that we've discovered the pattern, all we need to do is complete the sequence.
In order to identify which number comes after , we subtract and obtain the following:
In order to identify which number comes after , we subtract and obtain the following:
Let's complete the sequence:








