Area of Equilateral Triangles

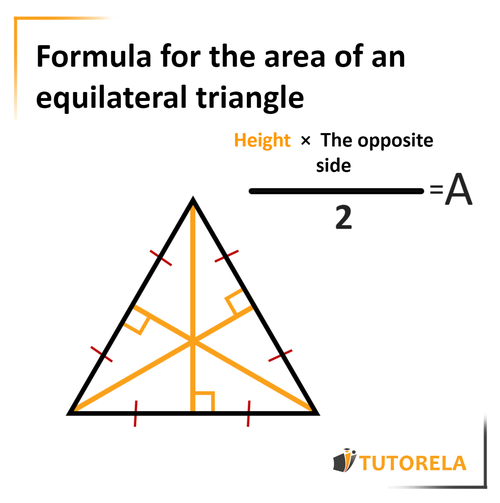
Formula to calculate the area of an equilateral triangle:

A - Formula for area of equilateral triangle

Detailed explanation

Start practice

Test yourself on area of a triangle!

Complete the sentence:

To find the area of a right triangle, one must multiply ________________ by each other and divide by 2.

Practice more now

Area of an Equilateral Triangle

Calculating the area of an equilateral triangle is quite simple, you can't get too confused with it, not even a little.
All you need to remember is the formula we will present to you below and apply it to equilateral triangles:

Remember!
In equilateral triangles, the height is also the median and the bisector.
Therefore, if the question only gives the length of the median or the bisector, you can immediately deduce that it is the height you need to place in the formula.
And on top of that, since the triangle is equilateral, you can immediately find the length of the edge (or side) corresponding. Simply compare it with the given edge since they are all equivalent.

Let's practice so we can understand even better how to calculate the area of an equilateral triangle:

Let's start with a classic exercise for beginners.

Given the triangle $\triangle ABC$

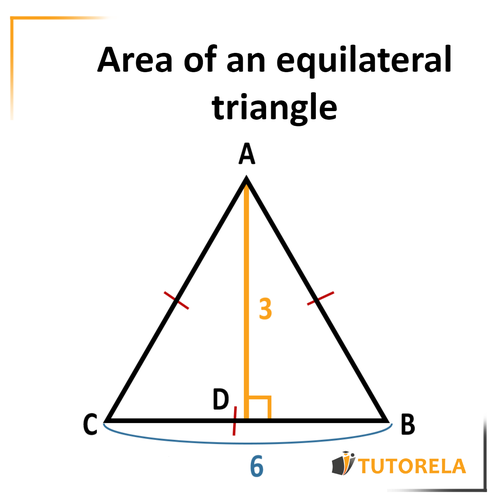
A2 - Practice of the area of the equilateral triangle

Given that:
$ABC$ Equilateral triangle
$AD=3$ Height
$CB= 6$

What is the area of the triangle?

Solution:
At first glance, we see that we have a height equivalent to $3$ and a side equivalent to $5$ .

Let's put it in the formula and we will obtain:
$\frac{6\times3}{2}=9$

Answer:

The area of the triangle $ABC$ is $9$ cm².

Simple and easy, right?

Join Over 30,000 Students Excelling in Math!

Endless Practice, Expert Guidance - Elevate Your Math Skills Today

Test your knowledge

Question 1

Calculate the area of the following triangle:

Question 2

Calculate the area of the following triangle:

Question 3

Calculate the area of the triangle using the data in the figure below.

Now let's move on to a more complicated exercise.

that covers various hypothetical situations that could confuse you on the exam:

Given the equilateral triangle $\triangle ABC$

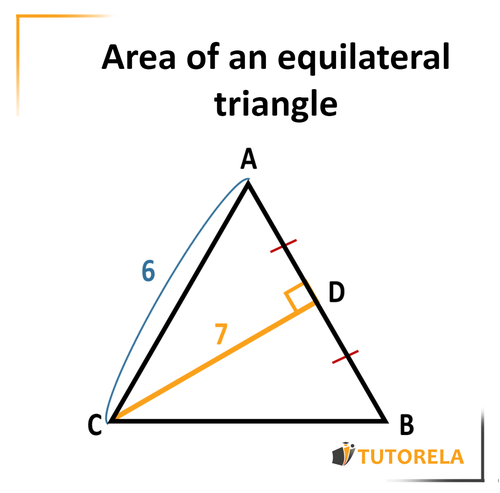
A3 - Practice of the area of the equilateral triangle

Given:
$AC = 6$
$DB=AD$
$CD=7$

What is the area of the triangle $\triangle ABC$ ?

Solution:

We know that to calculate the area of the triangle, we need to have the length of the height and the corresponding side with which it forms $90^o$ degrees.

In this exercise, it is not explicitly stated that $CD$ is the height of the triangle, but we know that: $AD =DB$ that is, $CD$ is the median - it crosses the side it touches, dividing it into two equal parts.
Since it is an equilateral triangle, the median is also the height of the triangle, and therefore, we can use it in the formula for calculating the area.
Additional note: If instead of the data that $CD$ is the median, they had given that it is the bisector $ABC$ , we could also have deduced that it is the height, since in an equilateral triangle, the median, the height, and the bisector coincide.

Therefore, we will note $CD=7$ as the height of the triangle.

Now we must find the length of the side $AB$
Since it is an equilateral triangle, all sides are equal, so we immediately deduce that $AB=AC = 6$
Now let's put it in the formula and we will get:

$\frac{6\times7}{2}=21$

Answer:
The area of the triangle $ABC$ is $21$ cm².

Examples and exercises with solutions for calculating the area of an equilateral triangle

Exercise #1

Calculate the area of the right triangle below:

Video Solution

Step-by-Step Solution

Due to the fact that AB is perpendicular to BC and forms a 90-degree angle,

it can be argued that AB is the height of the triangle.

Hence we can calculate the area as follows:

$\frac{AB\times BC}{2}=\frac{8\times6}{2}=\frac{48}{2}=24$

Answer

24 cm²

Exercise #2

Calculate the area of the following triangle:

Video Solution

Step-by-Step Solution

To find the area of the triangle, we will use the formula for the area of a triangle:

$\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$

From the problem:

The length of the base $BC$ is given as 7 units.
The height from point $A$ perpendicular to the base $BC$ is given as 4.5 units.

Substitute the given values into the area formula:

$\text{Area} = \frac{1}{2} \times 7 \times 4.5$

Calculate the expression step-by-step:

$\text{Area} = \frac{1}{2} \times 31.5$

$\text{Area} = 15.75$

Therefore, the area of the triangle is $15.75$ square units. This corresponds to the given choice: $15.75$ .

Answer

15.75

Exercise #3

What is the area of the triangle in the drawing?

Video Solution

Step-by-Step Solution

First, we will identify the data points we need to be able to find the area of the triangle.

the formula for the area of the triangle: height*opposite side / 2

Since it is a right triangle, we know that the straight sides are actually also the heights between each other, that is, the side that measures 5 and the side that measures 7.

We multiply the legs and divide by 2

$\frac{5\times7}{2}=\frac{35}{2}=17.5$

Answer

17.5

Exercise #4

Calculate the area of the triangle using the data in the figure below.

Video Solution

Step-by-Step Solution

To calculate the area of the triangle, we will follow these steps:

Identify the base, CB, as 6 units.
Identify the height, AC, as 8 units.
Apply the area formula for a triangle.

Now, let's work through these steps:

The triangle is a right triangle with base $CB = 6$ units and height $AC = 8$ units.

The area of a triangle is determined using the formula:

\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}

Substituting the known values, we have:

\text{Area} = \frac{1}{2} \times 6 \times 8

Perform the multiplication and division:

\text{Area} = \frac{1}{2} \times 48 = 24

Therefore, the area of the triangle is $24$ square units.

Answer

Exercise #5

Calculate the area of the triangle below, if possible.

Video Solution

Step-by-Step Solution

To solve this problem, we begin by analyzing the given triangle in the diagram:

While the triangle graphic suggests some line segments labeled with the values "7.6" and "4", it does not confirm these as directly usable as pure base or height without additional proven inter-contextual relationships establishing perpendicularity or side/unit equivalences.

Without a clear base and perpendicular height value, we cannot apply the triangle's area formula $\text{Area} = \frac{1}{2} \times \text{base} \times \text{height}$ effectively, nor do we have all side lengths for Heron's formula.

Therefore, due to insufficient information that specifically identifies necessary dimensions for area calculations such as clear height to a base or all sides' measures, the area of this triangle cannot be calculated.

The correct answer to the problem, based on insufficient explicit calculable details, is: It cannot be calculated.

Answer

It cannot be calculated.

Do you know what the answer is?

Question 1

Calculate the area of the triangle using the data in the figure below.

Question 2

Calculate the area of the following triangle:

Question 3

What is the area of the given triangle?

Start practice

Area of Equilateral Triangles

Test yourself on area of a triangle!

Area of an Equilateral Triangle

Let's start with a classic exercise for beginners.

Now let's move on to a more complicated exercise.

Examples and exercises with solutions for calculating the area of an equilateral triangle

Exercise #1

Video Solution

Step-by-Step Solution

Answer

Exercise #2

Video Solution

Step-by-Step Solution

Answer

Exercise #3

Video Solution

Step-by-Step Solution

Answer

Exercise #4

Video Solution

Step-by-Step Solution

Answer

Exercise #5

Video Solution

Step-by-Step Solution

Answer

More Questions

Area of a Triangle