Identification of an Isosceles Triangle

When we have a triangle, we can identify that it is an isosceles if at least one of the following conditions is met:

1) If the triangle has two equal angles - The triangle is isosceles.
2) If in the triangle the height also bisects the angle of the vertex - The triangle is isosceles.
3) If in the triangle the height is also the median - The triangle is isosceles.
4) If in the triangle the median is also the bisector - The triangle is isosceles.

Detailed explanation

Start practice

Test yourself on types of triangles!

In a right triangle, the side opposite the right angle is called....?

Practice more now

Identification of an Isosceles Triangle

Before we talk about how to identify an isosceles triangle, let's remember that it is a triangle with two sides (or edges) of the same length - This means that the base angles are also equal.
Moreover, in an isosceles triangle, the median of the base, the bisector, and the height are the same, that is, they coincide.

Let's see it illustrated

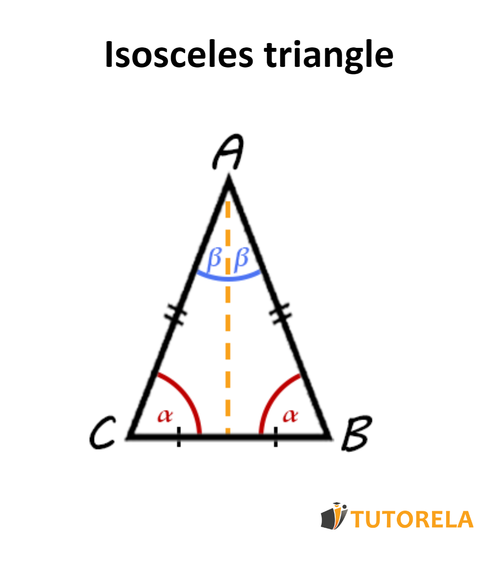
A - Identification of an isosceles triangle

These magnificent properties of the isosceles triangle cannot prove by themselves that it is an isosceles triangle.
So, how can we prove that our triangle is isosceles?

If at least one of the following conditions is met:
1) If our triangle has two equal angles - The triangle is isosceles.
This derives from the fact that the sides opposite to equal angles are also equal, therefore, if the angles are equal, the sides are too.

2) If in the triangle the height also bisects the vertex angle - The triangle is isosceles.
3) If in the triangle the height is also the median - The triangle is isosceles.
4) If in the triangle the median is also the angle bisector - The triangle is isosceles.
In fact, we can summarize guidelines $2$ and $4$ and write a single condition:
If two of these coincide - the median, the height, and the bisector - The triangle is isosceles.

Great, now you know how to identify isosceles triangles easily and quickly.

If you are interested in learning more about other angle topics, you can enter one of the following articles:

In the blog of Tutorela you will find a variety of articles about mathematics.

Examples and exercises with solutions for identifying an isosceles triangle

Exercise #1

In a right triangle, the side opposite the right angle is called....?

Step-by-Step Solution

The problem requires us to identify the side of a right triangle that is opposite to its right angle.
In right triangles, one of the most crucial elements to recognize is the presence of a right angle (90 degrees).
The side that is directly across or opposite the right angle is known as the hypotenuse. It is also the longest side of a right triangle.
Therefore, when asked for the side opposite the right angle in a right triangle, the correct term is the hypotenuse.

Selection from the given choices corroborates our analysis:

Choice 1: Leg - In the context of right triangles, the "legs" are the two sides that form the right angle, not the side opposite to it.
Choice 2: Hypotenuse - This is the correct identification for the side opposite the right angle.

Therefore, the correct answer is $\text{Hypotenuse}$ .

Answer

Hypotenuse

Exercise #2

In an isosceles triangle, what are each of the two equal sides called ?

Step-by-Step Solution

In an isosceles triangle, there are three sides: two sides of equal length and one distinct side. Our task is to identify what the equal sides are called.

To address this, let's review the basic properties of an isosceles triangle:

An isosceles triangle is defined as a triangle with at least two sides of equal length.
The side that is different in length from the other two is usually called the "base" of the triangle.
The two equal sides of an isosceles triangle are referred to as the "legs."

Therefore, each of the two equal sides in an isosceles triangle is called a "leg."

In our problem, we confirm that the correct terminology for these two equal sides is indeed "legs," distinguishing them from the "base," which is the unequal side. This aligns with both the typical definitions and properties of an isosceles triangle.

Thus, the equal sides in an isosceles triangle are known as legs.

Answer

Legs

Exercise #3

In a right triangle, the two sides that form a right angle are called...?

Step-by-Step Solution

In a right triangle, there are specific terms for the sides. The two sides that form the right angle are referred to as the legs of the triangle. To differentiate, the side opposite the right angle is called the hypotenuse, which is distinct due to being the longest side. Hence, in response to the problem, the sides forming the right angle are correctly identified as Legs.

Answer

Legs

Exercise #4

Is the triangle in the drawing a right triangle?

Step-by-Step Solution

Due to the presence of the 90 degree angle symbol we can determine that this is indeed a right-angled triangle.

Answer

Yes

Exercise #5

Is the triangle in the drawing an acute-angled triangle?

Video Solution

Step-by-Step Solution

An acute-angled triangle is defined as a triangle where all three interior angles are less than $90^\circ$ .

In examining the visual depiction of the triangle provided in the problem, we need to see if it appears to satisfy this property. The assessment relies on observing the triangle's structure shown in the drawing and noting any geometric indications suggesting angle types.

Given the information from the drawing, if all angles seem to satisfy the condition of being less than $90^\circ$ , then by definition, the triangle is an acute-angled triangle.

Conclusively, the answer to whether the triangle is acute-angled based on provided visual assessment and inherent assumptions in its illustration is: Yes.