A large number of the questions in geometry contain proofs. Therefore, one must study the correct and formal way to write them. When we are asked to prove a certain claim, in fact, we have to construct a series of arguments that, each of them, must be accompanied by some explanation or justification. The explanation or justification can be some data, calculation, or some theorem. Finally, the last argument of the proof is based on the previous ones and confirms what we wanted to prove.
We will illustrate this with a simple example.
Given the triangle . We must prove that the triangle is an isosceles triangle.
The Formal Proof
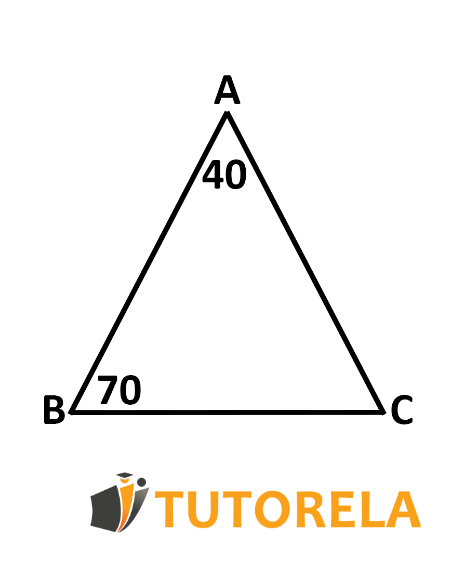
Let's start with the series of arguments:








