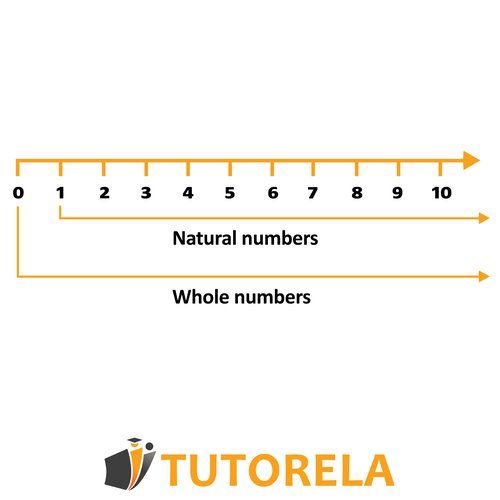
Whole numbers are positive or negative numbers that are integers – not fractions.
For a number to be called an integer, it must not be a fraction or a decimal number.
is considered an integer.
Whole Numbers
Integers
What is an integer?
Examples of whole numbers:

Integers
In this article, you will learn everything you need to know about integers and practice some exercises with integers.
Shall we begin?
What is an integer?
An integer is a positive or negative number that is not a fraction – in other words, a whole number.
Note: For a number to be an integer, it just needs to not be a fraction or a decimal. Simply a whole number, and it doesn't matter if it's positive or negative.
In arithmetic exercises, we use integers almost all the time and can use them with addition, subtraction, multiplication, or division operations.
And what about ?
is also an integer.
There are infinite integers: all positive and negative whole numbers from minus infinity to plus infinity are integers.
And now? Let's practice!
Find the integers from the following set of numbers:
Solution:
According to the definition, an integer is a positive or negative number that is not a fraction. Therefore:
: Integer – whole and positive.
: Integer – included in the set of integers.
: Integer – whole and negative.
: Not an integer – fraction.
It doesn't matter if it is positive or negative, as soon as it is a fraction, it is not an integer.
Find the integers from the following set of numbers:
Solution:
According to the definition, an integer is a positive or negative number that is not a fraction. Therefore:
: Integer – whole and positive
: Integer – it is negative and not positive
: Integer – negative and whole
Not an integer – fraction.
It doesn't matter that you can extract whole numbers from this fraction, an integer is a number that is entirely whole.
Find the natural numbers from the following set of numbers:
Solution:
: Not a whole number - a decimal number and not whole.
: Not a whole number – a decimal number and not whole
: Whole number – both positive and whole
: Not a whole number – even though there are whole parts, there is also the fraction, so it is called not whole.
Now, after we know how to identify whole numbers, let's move on to exercises with whole numbers:
Find what is in the square:
Solution:
In this exercise, where there are only whole numbers, we need to find out what appears as the square.
First, let's understand what the result of the parentheses gives us and rewrite the exercise. We get:
Now we can say that: times something equals .
If we subtract from both sides, we get:
Now let's think about what times will give us .
We can also simply divide both sides by and get that:
Another exercise with natural numbers:
The total price of one vase and cups is .
The price of one vase is equal to the price of cups.
- What is the price of one vase?
- What is the price of one cup?
Solution:
It is known that the price of one vase is equal to the price of cups.
If we call the price of one cup , we can say that the price of the vase is .
It is also known that one vase and cups cost .
We will write this as an equation and get:
We solve the equation and get:
Note – represents the price of one cup .
is the price of one vase .
If
then the answer will be:
the price of one pair of pants is .
the price of one shirt is .








