Thales' Theorem

According to Thales' theorem, if there are two parallel lines and one of them intersects the sides of a triangle, a proportion can be identified between the segments cut on the sides.
Let's see this in the diagram:

According to Thales' theorem –

If:
$DE∥CB$
then:
$\frac{AD}{DC} =\frac{AE}{EB}$

Note- The two lines must be parallel to satisfy Thales' theorem.
The triangle does not need to be isosceles at all. Notice that it's the ratio that is equal.

Additional note:
If it is true that:
$\frac{AD}{DC} =\frac{AE}{EB}$
We can determine that:
$DE∥CB$
According to the converse of Thales' theorem.

Exercise:

Given:
$DE∥CB$
AD=4
$DC=5$
$EB=7$
Find the length of $AE$

Solution
According to Thales' theorem, we can determine that if
$DE∥CB$
then
$\frac{AD}{DC} =\frac{AE}{EB}$

All segments are given except for $AE$. Let's call it $X$ and substitute the given data in the equation:
$AE=X$
$\frac{X}{7} =\frac{4}{5}$
Let's cross multiply and get:
$4\cdot7=5X$
$5X=28$
$X=5.6$
$AD= 5.6$
We found the length of $AD$.

The first extension of Thales' theorem states that:

If
$DE∥CB$
then:
$\frac{AD}{AC} =\frac{AE}{AB} = \frac{DE}{CB}$

Important emphasis:
Note that the denominators consist of the entire side and not just part of it.

Note:
If the following is true: $\frac{AD}{AC} =\frac{AE}{AB} = \frac{DE}{CB}$

We can determine that:
$\frac{AD}{AC} =\frac{AE}{AB} = \frac{DE}{CB}$
according to the converse of Thales' Extension Theorem 1.

Let's practice:

Given:
$DE∥CB$

$AB=8$
$AE=4$
$AC=6$
$CB=8$
Find the length of $DC$ and the length of $DE$

Solution:
According to the Extended Thales Theorem we know that:
$\frac{AD}{AC} =\frac{AE}{AB} = \frac{DE}{CB}$

Let's mark the given information in the figure to better understand what we need to do:

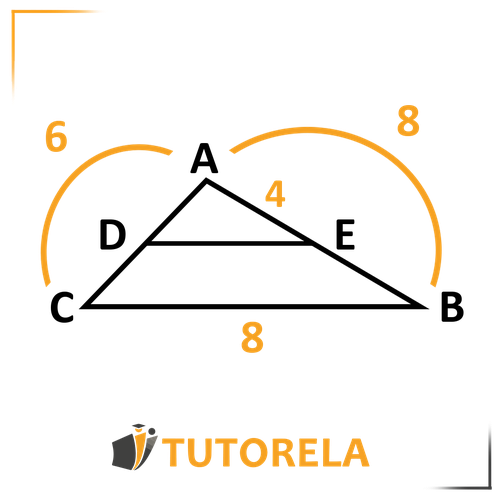
According to this ratio:
$\frac{AD}{AC} =\frac{AE}{AB}$
We can find $AD$ and thus get the length of $DC$ which we need to find.

Let's substitute the data in the relevant ratio and call $AD$ as $X$
$\frac{X}{6} =\frac{4}{8}$

Let's multiply crosswise and get:
$8X=24$
Divide by $8$ and get:
$X=3$
From this we determine that: $AD=3$
From here we can determine that if $6=AC$ and $AD=3$
then $3=DC$ because the whole equals the sum of its parts.

Now we'll move on to finding $DE$
According to this ratio $\frac{AE}{AB} = \frac{DE}{CB}$
Let's substitute the given values and let $DE =X$
We get:
$\frac{X}{8} =\frac{4}{8}$
We can determine that $X=4$
Therefore $DE=4$

According to the second extension of Thales' theorem

If
$AB∥DC$
then:

$\frac{DC}{AB} =\frac{DE}{EB} = \frac{CE}{EA}$

Pay attention -
This hourglass shape can appear as a trapezoid or circle as part of an exercise in a question.
When you identify such an "hourglass," know that there's a high chance you'll need to use the Extended Thales' Theorem.

Note:
If it holds that:

$\frac{DC}{AB} =\frac{DE}{EB} = \frac{CE}{EA}$

We can determine that:
$AB∥DC$
according to the converse of Thales' Extended Theorem.

Exercise:

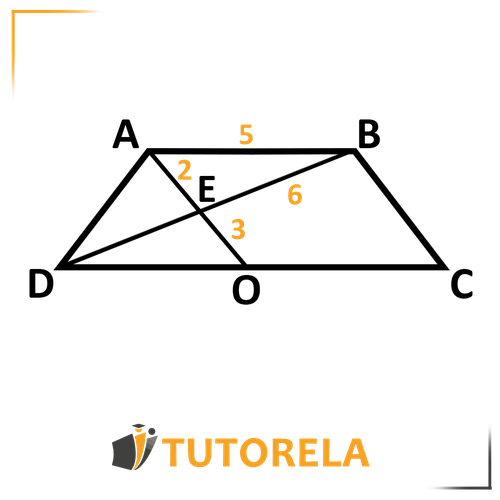
Given:
$ABCD$ is a trapezoid
$AO$ is a median to side $DC$
$AB=5$
$AE=2$
$OE=3$
$EB=6$
Find the length of $DE$
and the length of $DC$

Solution:
From the illustration, we can identify the "hourglass" and understand that we'll probably need to use the extended Thales theorem.
We are given that $ABCD$ is a trapezoid, so we can conclude that:
$AB∥DC$
And therefore:
$AB∥DO$
Since $DO$ is part of $DC$

According to the Extended Thales' Theorem:
$\frac{AE}{EO} =\frac{BE}{DE}$
We have all the data except for $DE$ which we'll call $X$.
Let's substitute in the equation and get:
$\frac{X}{6} =\frac{2}{3}$

Let's multiply crosswise and get:
$2X=18$
$X=9$
Therefore: $9=DE$
Now let's find $DC$.
Since $AO$ is a median, we'll find $DO$ using the extended Thales theorem II and multiply it by $2$ to get $DC$
According to extended Thales theorem II:
$\frac{AB}{DO} =\frac{AE}{EO}$
Let's substitute the given values and let $X=DO$
We get:
$\frac{X}{5} =\frac{2}{3}$
$2X=15$
$​​​​​​​X=7.5$
$DO=7.5$
Therefore: $DC =15$