Midsegment - Examples, Exercises and Solutions

Midsegment

The midsegment is a segment that connects the midpoints of 2 sides.
It's very simple to remember the meaning of this term since the word "middle" already tells us that it is about the midpoint, so when we come across the concept of "midsegment" we'll remember that it connects the midpoints of two sides.
We're here to teach you everything you need to know about the midsegment, from the proof to the wonderful properties of the segment that will help us solve exercises.
First, we'll talk about the midsegment of a triangle and then we'll move on to the midsegment of a trapezoid.

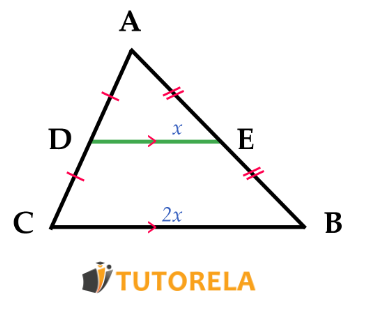
Midsegment of a Triangle

The midsegment of a triangle crosses the middle of two sides, is parallel to the third side
and is also half its length.

We can demonstrate that a midsegment exists in a triangle if at least one of the following conditions is met:

1. If there is a straight line in a triangle that extends from the midpoint of one side to the midpoint of another side, we can determine that this is a midsegment, and therefore, it is half the length of the third side and is also parallel to it.
2. If a straight line cuts one of the sides of a triangle and is parallel to another side of the triangle, it indicates that this is a midsegment and that it also cuts the third side of the triangle in half and is half the length of the side to which it is parallel.
3. If there is a segment in a triangle whose ends are on two of its sides, is half the length of the third side, and is parallel to it, we can determine that this segment is a midsegment and, therefore, it bisects the sides it touches right in the middle.

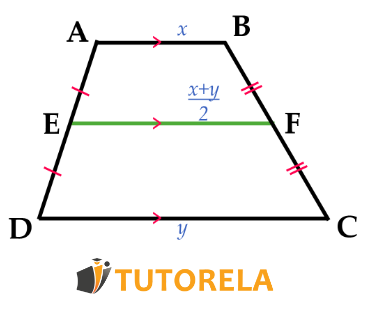
Midsegment of a Trapezoid

The midsegment of a trapezoid divides the two sides it originates from into two equal parts, and is also parallel to both bases of the trapezoid and measures half the length of these bases.

We can demonstrate that there is a midsegment in a trapezoid provided that, at least, one of the following conditions is met:

1. If there is a straight line in a trapezoid that extends from the midpoint of one side to the midpoint of another side, we can determine that it is a midsegment. As a result, it is parallel to both bases of the trapezoid and its length is half that of these bases.
2. If there is a straight line that extends from one side of a trapezoid and is parallel to one of the trapezoid's bases, we can confirm that it is a midsegment. Therefore, it is parallel to both bases of the trapezoid, its length is half that of these two bases, and it also bisects the second side that it touches.