Volume Units - Examples, Exercises and Solutions

Every three-dimensional body has volume. For example, a ball or pyramid are bodies with volume. The volume of a body is our way of measuring the space that said body occupies in space.

For example, let's observe a cube whose length of each of its sides is $1\operatorname{cm}$, like this one:

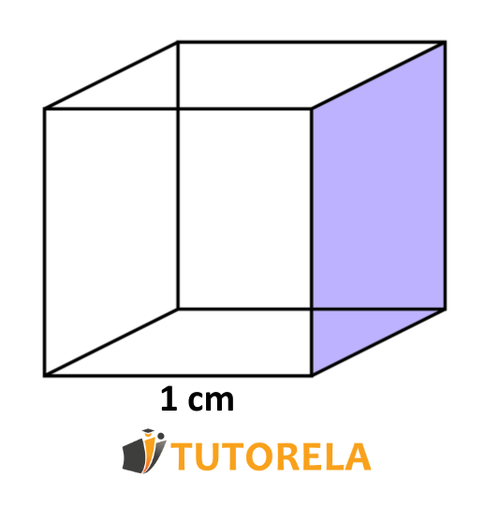
To calculate the volume of the cube we will use the known formula: $Length\times ~width\times~height$

In this case, the three dimensions are equal and, therefore, we will note:

$V=1\operatorname{cm}\times1\operatorname{cm}\times1\operatorname{cm}=1\operatorname{cm}^3$

V is the letter used to abbreviate the word volume in exercises and is used to designate volumes.

That is, we found that the volume of the cube is $1~cm³=$ cubic centimeter (cm raised to the third power)

Known volume measurement units:

$1~m³=1000~dm³=1,000,000~cm³$

$1~dm³=1000~cm³$

Additionally, there are measurements that we primarily use for measuring liquids:

$1~L=1~dm³=1,000~cm³$

$1~liter=1000~milliliters$

$1~milliliter = 1~cm³$

$1000~liters=1~m³$