The definition of a logarithm is:
Subtraction of Logarithms
Subtraction of Logarithms
Where:
is the base of the exponent
is what appears inside the log, can also appear in parentheses
is the exponent we raise the log base to in order to obtain the number that appears inside of the log.
Subtraction of logarithms with identical base is based on the following rule:
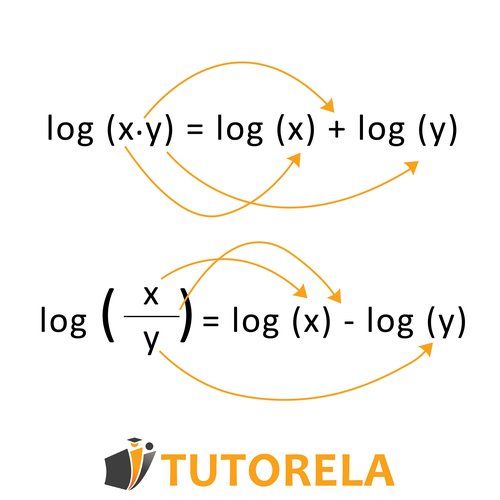
Subtraction of logarithms with different bases is performed by changing the base using the following rule:

Test yourself on subtraction of logarithms!
\( \log_53-\log_52= \)
Subtraction of Logarithms
Reminder - Logarithms
First, let's recall what is the definition of ?
Where is the base of the log (usually )
is the exponent we raise to
is the number that appears inside the log, sometimes in parentheses, and it's the number that we get when is raised to the power of
meaning:
For example, if we have an exercise like this:
Determine which power we need to raise to in order to obtain....?
The answer is to the power of and therefore the solution is .
Subtraction of logarithms with the same base
To easily subtract logarithms with the same base, all you need to know is the following rule about subtracting logarithms with identical bases:
The rule states that if you want to subtract logs with the same base, you can write them as log and divide the numbers inside the log. This will sometimes make it easier to solve.
Note - The numerator will always be the first log from which we subtract, and the denominator will always be the second log that we subtract from the original.
Let's look at an example:
At first glance, this problem looks intimidating. However you'll soon see how using the subtraction rule for identical logarithms makes it simple.
Which power should we raise to in order to obtain ?... Which power should we raise to in order to obtain ?
All we need to do is divide the numbers that appear in the logarithm while keeping the base the same - .
Of course, we'll do this in order - in the numerator we'll put the first number and in the denominator we'll put the second number .
We obtain the following:
As well as:
Now it's much easier for us to solve the equation!
We know that we need to raise to the power of to obtain and therefore the entire answer to this problem is .
Note - this rule is only valid in cases where the base is identical. If the base was not the same in both logarithms, we could not use this rule.
\( \log_29-\log_23= \)
\( \log_75-\log_72= \)
\( \frac{1}{5}\log_81024-2\log_8\frac{1}{2}= \)
Subtraction of logarithms with the same base
What happens when there is a subtraction exercise with logarithms and different bases?
In order to subtract logs with different bases, you need to use the log base change rule.
The goal is - to convert both logs to the same base.
How do you change the base of a logarithm?
Meet the change of base formula for logs.
And now for the explanation:
When we have a log with base and we want to convert it to another log, we will always convert it to a fraction in the following way:
- Draw a fraction line.
- In the numerator, write the logarithm with the desired new base as well as what was in the original logarithm.
- In the denominator, write the logarithm with the desired new base where the inside of the logarithm will be the base of the original logarithm.
Let's look at an example:
Convert the following logarithm to base :
In the numerator we'll write the log with base , the base we want to convert to. The number inside the log in the numerator will be the original number that appears inside the log - which is .
In the denominator, we will write again log base , the base we want to convert to, but this time, the number inside the log will be the original base - which is
Now we can solve the problem easily. We will obtain the following answer:
Advanced exercise:
Now you can solve logarithm subtraction with different bases:
We want to convert both logarithms to the same base, and usually we choose the smaller base - .
Therefore:
Let's now rewrite the exercise and insert the data that we obtained:
Let's insert
and obtain the following:
\( \frac{1}{2}\log_39-\log_31.5= \)
\( \frac{1}{4}\cdot\log_61296\cdot\log_6\frac{1}{2}-\log_63= \)
\( \log_7x^4-\log_72x^2=3 \)
?=x
Examples with solutions for Subtraction of Logarithms
Exercise #1
Video Solution
Step-by-Step Solution
To solve the problem, we employ the property of logarithms for subtraction:
- Step 1: Recognize the expression .
- Step 2: Apply the logarithmic property for subtraction, .
- Step 3: Substitute into the property: .
By applying the property, we simplify the expression to . This is equivalent to . Therefore:
Therefore, the result of the expression is .
Answer
Exercise #2
Video Solution
Step-by-Step Solution
To solve the problem of evaluating , we apply the properties of logarithms as follows:
- Step 1: Recognize that the expression uses a subtraction of logarithms with the same base: .
- Step 2: Use the logarithmic subtraction rule: .
- Step 3: Simplify using this rule: .
- Step 4: Perform the division: .
- Step 5: Therefore, .
Thus, the simplified and evaluated result is .
Answer
Exercise #3
Video Solution
Step-by-Step Solution
To solve the problem, let's use the rules of logarithms:
- Step 1: Recognize that we are dealing with the subtraction of logarithms sharing the same base, which calls for the identity .
- Step 2: Apply this identity to the expression .
- Step 3: Realize that this can thus be expressed as a single logarithm: .
- Step 4: Simplify the fraction, yielding .
Therefore, the simplification results in the expression: .
This matches the correct answer from the given choices.
Answer
Exercise #4
Video Solution
Step-by-Step Solution
To solve this problem, we'll begin by simplifying the given expression using logarithmic rules:
- Step 1: Simplify the first term :
Since , we can rewrite this as . Thus, . - Step 2: Simplify the second term :
Note . Therefore, . Thus, . - Step 3: Subtract the expressions:
Combine the terms using the difference rule:
. - Step 4: Simplify further:
Since , we can express this as .
Therefore, the simplified form of the expression is .
The correct choice is thus , matching with choice (1).
Answer
Exercise #5
Video Solution
Step-by-Step Solution
To solve the problem , we need to apply the rules of logarithms:
- **Step 1: Simplify with the power rule**
Using the power rule . Since , we have . Thus, . - **Step 2: Apply the subtraction rule**
Now, the expression becomes . Using the subtraction rule: . - **Step 3: Simplify the fraction**
Calculate : it simplifies to 2 because .
Thus, the simplified expression is .
Using the provided answer choices, the correct answer matches choice , which corresponds to choice 2.
Therefore, the solution to the problem is .
Answer
More Questions
Subtraction of Logarithms
- Solve the Logarithmic Equation: log₃(x²)log₅(27) - log₅(8) = ln(e)
- Solve the Multi-Base Logarithm Equation: log₆₄ × log₉x = (log₆x² - log₆x)(log₉2.5 + log₉1.6)
- Solve the Logarithmic Equation: Base-8 and Base-4 Logs with Quadratic Terms
- Solve Complex Logarithmic Equation: log₅9(log₃4x + log₃(4x+1)) = 2(log₅4a³ - log₅2a)
- Solve Complex Logarithm Equation: Product of Log_a(x), Log_b(y), and Log_c(2)









