Find Side BC in Right Triangle: Given Sides 2 and 7

Q: How do I know which side is the hypotenuse?

The hypotenuse is always the longest side and sits opposite the right angle. In this diagram, side AC (length 7) is the hypotenuse because it's diagonal across from the right angle at B.

Q: Why can't I just use a calculator for √45?

Calculators give decimal approximations like 6.708, but math problems often want exact answers in simplest radical form. $ 3\sqrt{5} $ is the exact, simplified form.

Q: How do I simplify square roots?

Look for perfect square factors! Factor the number under the radical: $ \sqrt{45} = \sqrt{9 \times 5} $. Since $ \sqrt{9} = 3 $, you get $ 3\sqrt{5} $.

Q: Can I check my answer?

Yes! Substitute back: $ 2^2 + (3\sqrt{5})^2 = 4 + 9(5) = 4 + 45 = 49 $. Since $ 7^2 = 49 $, your answer is correct!

Q: What if I get the sides mixed up?

Always identify the right angle first (look for the square symbol). The hypotenuse is opposite this angle. In this problem, sides AB = 2 and BC = ? are legs, while AC = 7 is the hypotenuse.

Pythagorean Theorem with Radical Simplification

Look at the triangle in the diagram. How long is side BC?

❤️ Continue Your Math Journey!

We have hundreds of course questions with personalized recommendations + Account 100% premium

Step-by-step video solution

Watch the teacher solve the problem with clear explanations

00:05 Let's find the length of side B C.

00:08 We'll use the Pythagorean theorem since we have a right triangle.

00:15 Now, let's substitute the values we know and solve for B C.

00:24 Next, let's isolate C B in our equation.

00:27 Extract the square root to find the exact length.

00:36 Break down 45 into factors of 9 and 5.

00:42 And there you have it! That's how we find the solution.

Step-by-step written solution

Follow each step carefully to understand the complete solution

Understand the problem

Look at the triangle in the diagram. How long is side BC?

Step-by-step solution

To solve the exercise, it is necessary to know the Pythagorean Theorem:

A²+B²=C²

We replace the known data:

2²+B²=7²

4+B²=49

We input into the formula:

B²=49-4

B²=45

We find the root

B=√45

This is the solution. However, we can simplify the root a bit more.

First, let's break it down into prime numbers:

B=√(9*5)

We use the property of roots in multiplication: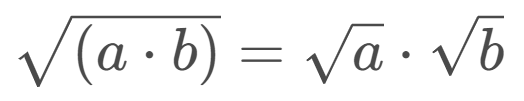

B=√9*√5

B=3√5

This is the solution!

Final Answer

$3\sqrt{5}$ cm

Key Points to Remember

Essential concepts to master this topic

Pythagorean Theorem: For right triangles, $a^2 + b^2 = c^2$ where c is hypotenuse
Technique: Substitute known values: $2^2 + BC^2 = 7^2$ gives $BC^2 = 45$
Simplification Check: $\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}$ ✓

Common Mistakes

Avoid these frequent errors

Not simplifying the radical answer
Don't leave your answer as $\sqrt{45}$ = wrong form! This isn't fully simplified and won't match answer choices. Always factor out perfect squares: $\sqrt{45} = \sqrt{9 \times 5} = 3\sqrt{5}$ .

Practice Quiz

Test your knowledge with interactive questions

Look at the triangle in the diagram. How long is side AB?

FAQ

Everything you need to know about this question

How do I know which side is the hypotenuse?

The hypotenuse is always the longest side and sits opposite the right angle. In this diagram, side AC (length 7) is the hypotenuse because it's diagonal across from the right angle at B.

Why can't I just use a calculator for √45?

Calculators give decimal approximations like 6.708, but math problems often want exact answers in simplest radical form. $3\sqrt{5}$ is the exact, simplified form.

How do I simplify square roots?

Look for perfect square factors! Factor the number under the radical: $\sqrt{45} = \sqrt{9 \times 5}$ . Since $\sqrt{9} = 3$ , you get $3\sqrt{5}$ .

Can I check my answer?

Yes! Substitute back: $2^2 + (3\sqrt{5})^2 = 4 + 9(5) = 4 + 45 = 49$ . Since $7^2 = 49$ , your answer is correct!

What if I get the sides mixed up?

Always identify the right angle first (look for the square symbol). The hypotenuse is opposite this angle. In this problem, sides AB = 2 and BC = ? are legs, while AC = 7 is the hypotenuse.

🌟 Unlock Your Math Potential

Get unlimited access to all 18 Pythagorean Theorem questions, detailed video solutions, and personalized progress tracking.

📹

Unlimited Video Solutions

Step-by-step explanations for every problem

📊

Progress Analytics

Track your mastery across all topics

🚫

Ad-Free Learning

Focus on math without distractions

No credit card required • Cancel anytime

Find Side BC in Right Triangle: Given Sides 2 and 7

Pythagorean Theorem with Radical Simplification

❤️ Continue Your Math Journey!

Step-by-step video solution

Step-by-step written solution

Understand the problem

Step-by-step solution

Final Answer

Key Points to Remember

Common Mistakes

Practice Quiz

FAQ

How do I know which side is the hypotenuse?

Why can't I just use a calculator for √45?

How do I simplify square roots?

Can I check my answer?

What if I get the sides mixed up?

🌟 Unlock Your Math Potential

More Questions

Using the Pythagorean Theorem

Calculate Triangle Side AC: Using 3-4 Right Triangle Measurements

Right Triangle Side Length: Find BC Given Sides 5 and 13

Calculate Side AB in a Right Triangle: Given Sides 2 and 3

Find Circle Area: Perpendicular Radii with Distance y+2

Pythagorean Theorem

Finding Length DB in a Complex Triangle Configuration: 6-Unit Height Problem

Solve the Triangle Ratio Problem: Finding a and b with a + b = 7

Calculate Rectangle Area: Finding ABGE with Given Measurements 5cm and 3cm

Compare Perimeter vs Circumference: Triangle (5-6) vs Circle (Radius 6)